


Next: The tile model
Up: Foundational models and abstract
Previous: Sequentiality
In Confer-1, Action structures have been proposed as an algebra for
both the syntax and the semantics of interactive computation.
Action calculi are action structures of a concrete nature, with added
structure, and which represent a wide variety of calculi of
computation - functional, sequential, and concurrent. Each action in
an action calculus is represented as an assembly of molecules; the
syntactic binding of names is the means by which molecules are bound
together. One action calculus differs from another only in its
generators, called controls. The work on action calculi has been
pursued this year in Cambridge in the following directions:
- Labelled transition systems and bisimulation
congruences The semantics of a process calculus, several of which
have been introduced during CONFER, can often be most intuitively
given as a reduction relation, defined by a structural congruence and
reduction axioms. The action calculus framework embraces a rather wide
class of such definitions. A central problem is then that of
deriving, from such a definition of reduction, a labelled transition
semantics for which bisimulation is a satisfactory congruence.
Considerable progress has been made, e.g. by Jensen
[Jen98] for a form of graph rewriting approximating to a
graphical presentation of action calculi, and by Sewell for special
cases of term rewriting. Work on more general cases is being
undertaken by Gardner, Jensen, Leifer, Milner and Sewell.
- Expressiveness A uniform framework for the operational
semantics of calculi allows comparisons of expressiveness to be made.
Using natural homomorphisms between control structures (the models of
action calculi), it is possible to characterise important properties
of calculi such as mobility of channels. Leifer has shown
that the
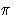 -calculus is mobile in this sense, whilst many other calculi such
as CCS, the
-calculus is mobile in this sense, whilst many other calculi such
as CCS, the 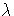 -calculus, and Petri nets, are not. This work, extending the
work of Mifsud at Edinburgh, gives a precise meaning to the intuitive
sense in which the
-calculus, and Petri nets, are not. This work, extending the
work of Mifsud at Edinburgh, gives a precise meaning to the intuitive
sense in which the 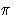 -calculus is more expressive than, say, CCS.
-calculus is more expressive than, say, CCS.
-
Gardner has introduced a type-theoretic description of action
calculi [GH97] which develops her previous work on a name-free
account of action calculi and gives a logical interpretation based on
the general binding operators studied by Aczel. With her Ph.D student
Hasegawa, at Edinburgh, she has shown that the type-theoretic account
of higher-order action calculi corresponds to Moggi's commutative
computational
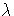 -calculus. With Gordon Plotkin and Andrew
Barber, also at Edinburgh, they have introduced a further extension of
action calculi, called the linear action
calculi [BGHP97]. Linear action calculi extend the higher-order
case, and the associated type theory corresponds to the linear type
theories studied by Barber and Nick Benton of Cambridge. The
conservative extension results follow from looking at the
corresponding categorical models.
-calculus. With Gordon Plotkin and Andrew
Barber, also at Edinburgh, they have introduced a further extension of
action calculi, called the linear action
calculi [BGHP97]. Linear action calculi extend the higher-order
case, and the associated type theory corresponds to the linear type
theories studied by Barber and Nick Benton of Cambridge. The
conservative extension results follow from looking at the
corresponding categorical models.
- Examples Several example action calculi have been
considered, including a functional programming language with mutable
store and exceptions, the ambient calculus of Abadi and Cardelli, and
distributed process calculi.
- Higher-order reflexive action calculi The first of
these examples required two previously separate enrichments of AC,
namely, the higher-order and the reflexive extensions (the latter in a
simplified form). The proof that an AC combining the two is
well-defined reduces to a proof of strong normalisation for the
higher-order beta-reduction of the molecular forms corresponding to
this enriched AC. Leifer completed this proof and, in the process of
doing so, developed several new techniques for handling molecular
forms, including the formalisation of manipulations involving
reflexive substitutions.
[[BGHP97]]
Andrew Barber, Philippa Gardner, Masahito Hasegawa, and Gordon Plotkin.
From action calculi to linear logic,.
In Proceedings of CSL 97, Aarhus, 1997.
[[Gar98]]
Philippa Gardner.
Closed action calculi.
Theoretical Computer Science, 1998.
To appear.
[[GH97]]
Philippa Gardner and Masahito Hasegawa.
Types and models in higher-order action calculi.
In Proceedings of TACS 97, Sendai, Japan, 1997.
[[Jen98]]
Ole Høgh Jensen.
PhD thesis, University of Cambridge.
Forthcoming, 1998.



Next: The tile model
Up: Foundational models and abstract
Previous: Sequentiality
1/10/1998
![]()
![]()
![]()
![]()