Quake

Sujet proposé par Jean-Jacques Lévy

`Jean-Jacques@inria.fr`

Beaucoup de jeux font intervenir un joueur comme un guerrier bien armé se déplaçant en temps-réel dans un univers plus ou moins sympathique. Quake, Shadow Warrior, Unreal Tournament, Marathon, Rune, Deep Space Nine: the Fallen, etc, mais autrefois Maze War, en sont les exemples emblématiques. Plus pacifiquement, on peut aussi imaginer un joueur circulant dans un musée virtuel à visiter interactivement en découvrant ses multiples trésors. Le graphisme de ces jeux s'est fortement amélioré au cours de ces dernières années, principalement à cause de l'augmentation de la vitesse des ordinateurs et grâce aux performances toujours accrues de leurs cartes graphiques. Initialement, le graphisme était relativement simple, l'utilisateur ne voyant que des textures sur quelques murs (et le bout de son arme ...). La particularité de ces jeux est que le décor est quasiment immobile, seul le joueur se déplace à grande vitesse dans ce labyrinthe. Bien sûr, il peut apparaître (plutôt rarement) quelques créatures ou objets nouveaux.

Informatiquement, on résoud un problème de graphique à deux dimensions (et demi). Un grand ensemble de murs verticaux est supposé fixe et donné. Le joueur se déplace horizontalement (en pouvant parfois sauter -- d'où la demi-dimension supplémentaire) au milieu de ces murs. Il faut donc créer une illusion de 3D en calculant en temps-réel les faces du décor visibles par l'observateur avec une certaine texture et un pseudo effet de perspective.

1 Principe général

1.1 Arbres BSP

Les arbres BSP (Binary Space Partition) sont une représentation d'un ensemble de n hyperplans dans un espace à k dimensions destinée à faciliter le calcul des faces visibles à partir de tout point d'observation. Nous prendrons le cas où k=2 et considérerons la représentation d'un ensemble de n segments. Intuitivement, il s'agit d'une vue aérienne des murs verticaux de notre labyrinthe.

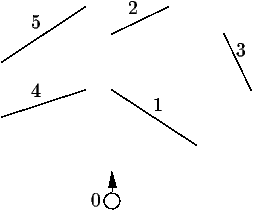
Dans la figure, l'observateur 0 ne voit que les murs 1, 4 et un bout du mur 5, puisque 2, 3 et 5 sont cachés par 1 et 4. Pour trouver efficacement l'ensemble visible depuis l'observateur (quelle que soit sa position), on construit un arbre BSP dont les noeuds sont les murs et tel que pour tout noeud i, le sous-arbre de gauche et le sous-arbre de droite ne contiennent que des murs du même coté de i. Donc tout noeud i d'un arbre BSP partitionne l'ensemble de ses sous-arbres par rapport à la droite s'appuyant sur le mur i. Ainsi dans notre exemple, si 1 est la racine de l'arbre, les murs 2 et 3 se retrouvent d'un même coté, et 4 du coté opposé. Pour 5, la situation est plus délicate puisque la droite s'appuyant sur le mur 1 coupe le mur 5. 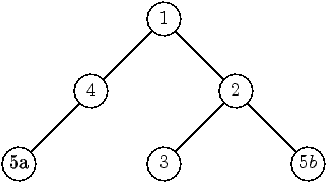Il faut donc éclater 5 en deux murs 5a et 5b, pour ranger 4 et 5a dans le sous-arbre de gauche de 1, et 2, 3 et 5b dans le sous-arbre de droite de 1. Récursivement, 5b est d'un coté de 2, et 3 de l'autre coté de 2. Enfin, 5a est d'un seul coté de 4. On aboutit ainsi à l'arbre de la figure suivante.

L'orientation par rapport à tout noeud est arbitraire. Il suffit d'avoir sa propre convention. Dans notre exemple, l'arbre de gauche est orienté vers les sud pour 1 et 2, mais pas pour 4. De toutes façons, il faudra bien une convention pour les murs nord-sud. De même, l'ordre dans lequel les segments sont rangés dans l'arbre est arbitraire. Pourtant, le nombre d'éclatements de murs (et donc la taille de l'arbre) peut en dépendre.

1.2 Rendu des images

Pour calculer les faces visibles à partir de l'observateur 0, on utilise l'algorithme du peintre, qui consiste à afficher les murs de l'arrière vers l'avant par rapport à la position de l'observateur. L'arbre BSP est justement construit pour optimiser l'algorithme du peintre, puisqu'on trouve rapidement l'ordre dans lequel les murs doivent être peints.

Pour afficher chaque mur, il suffit de créer une ligne d'horizon artificiel, et de dessiner chaque mur comme un trapèze avec une pseudo-perspective. Dans la figure suivante, on suppose un ciel blanc, un sol assez foncé, et des murs bleus avec l'observateur étant supposé à mi-hauteur des murs. Tout le problème du rendu est de faire un judicieux équilibre entre le réalisme de la figure et la vitesse d'exécution.

1.3 Graphique interactif

Il faut disposer d'opérations relativement efficaces pour lire la position de la souris et pour peindre des trapèzes ou des rectangles. A priori, tous les langages contiennent des fonctions graphiques dans leur bibliothèque pour de telles opérations. En Java, il est conseillé d'utiliser la bibliothèque standard AWT dont la documentation est en-ligne. Mais le projet peut aussi être fait dans d'autres langages selon les gouts. Comme exemple d'efficacité possible en Java, il suffit de consulter la page Web

http://symbolcraft.com/graphics/bsp/index.html

aussi disponible en

http://jeanjacqueslevy.net/bsp/

En Ocaml, on peut aussi voir OcamlQuake de François Pessaux en
http://pauillac.inria.fr/~pessaux/creations_fr.html

La documentation en ligne sur le graphique en Java peut être obtenue à partir de la page du cours : http://www.enseignement.polytechnique.fr/informatique/IF_TDS/

2 Travail demandé

Il faut donc écrire un programme qui réalise les fonctions suivantes:

la construction des arbres BSP à partir d'une entrée texte ou graphique. (Les segments peuvent être rentrés à la souris en cliquant sur les deux extrémités.) La construction peut chercher à minimiser la taille de l'arbre.
l'affichage de l'arbre BSP pour visualiser la structure sur laquelle on travaille.
l'affichage 3D des murs vus de l'observateur en utilisant l'algorithme du peintre.
l'affichage d'une vue aérienne pour comprendre en temps-réel la position de l'observateur dans le labyrinthe.
le déplacement de l'observateur au milieu des murs. Ce déplacement doit à la fois changer le point courant et l'orientation du sens d'observation (représenté par une flèche dans notre exemple). On cherchera à rendre ce déplacement interactif pour donner l'impression que le projet peut servir de support à un jeu. Le rapport entre la dimension du labyrinthe et la vitesse d'exécution est à démontrer.

3 Extensions

Toutes les extensions vers les jeux sont possibles. Par exemple:

introduire des personnages ou obstacles ou trésors dans le labyrinthe, dont le déplacement peut être plus ou moins aléatoire (robots).
travailler le rendu pour donner une texture plus réaliste aux murs
interconnecter les programmes pour faire un jeu distribué. (Cette extension est difficile et nécessite des connaissances en programmation des systèmes et des réseaux).
travailler en 3D plutôt qu'en 2D et demi.
aller aux cours de François Sillion, Philippe Chassignet ou Olivier Devillers, en majeures Informatique.

Références

[1]: M. de Berg, M. van Kreveld, M. Overmars, O. Schwarzkopf, Computational Geometry, Algorithms and Applications, Springer, (2000), 2ème édition.
[2]: J.-D. Boissonnat, M. Yvinnec, Géométrie Algorithmique, EdiScience international (1995).
[3]: F.P. Preparata, M.I. Shamos, Computational Geometry: an Introduction, Springer, New York, NY, (1985).
[4]: R. Sedgewick, Algorithms, Addison-Wesley, Reading, Ma, (1983).

Ce document a été traduit de L^AT_EX par H^EV^EA.