Contrôle Classant -- Informatique 431

Claire Kenyon   Jean-Jacques Lévy 1
Ecole polytechnique, 30 juin 2005






On attachera une grande importance à la concision, à la clarté, et à la précision de la rédaction. Lorsqu'une question porte sur une complexité en temps ou en espace, seul l'ordre de grandeur en fonction du paramètre précisé est demandé, dont on demande une démonstration à chaque fois.



Une entreprise de distribution ouvre plusieurs magasins dans une nouvelle région à commercialiser. Les sites de ses magasins doivent être optimisés en fonction de plusieurs facteurs: 1/ la somme des distances parcourues par les clients pour se rendre au magasin le plus proche; 2/ le coût d'ouverture des magasins; 3/ le maximum des distances parcourues par les clients pour se rendre au magasin le plus proche.

Pour simplifier, on suppose qu'il n'y a qu'un seul client par site et que les magasins ne s'installent que sur les sites des clients. Ainsi, si X = {x0, x1, ... xn-1} est l'ensemble des n sites clients (n > 0), on veut ouvrir k magasins (k > 0) sur des sites yj tels que l'ensemble Y = {y0, y1, ... yk-1} vérifie Y Í X.

Soit d(xi,xj) la distance entre les sites xi et xj et coût(xi) le coût d'ouverture d'un magasin sur le site xi. On cherchera d'abord à minimiser, pour tous les sous-ensembles Y de k élements dans X, la quantité S(Y) suivante:
S(Y) = d(x0, Y) + d(x1, Y) + ··· + d(xn-1, Y) + coût(Y)
avec   d(xi,Y) = min{d(xi,yj) | yj Î Y}   et  coût (Y) =
 
å
yj Î Y
coût(yj)
où d(xi,Y) est la distance minimale parcourue par le client i pour se rendre à un magasin situé dans Y, et coût(Y) est la somme des coûts d'ouverture des magasins situés en Y.

Dans ce problème, on utilisera les classes Paire (dans la partie I), Liste et Graphe (dans les parties III et IV) pour définir des paires d'entiers, des listes de paires, et des graphes non-orientés représentés par un tableau de listes qui donne pour chaque sommet s, la liste des paires (t, l) pour chaque arc allant de s à t de longueur l.

  int un; int deux;
  Paire (int x, int y) {
    un = x; deux = y;
} }

class Liste {
  Paire val; Liste suivant;
  Liste (Paire x, Liste ls) {
    val = x; suivant = ls;
} }
  Liste[ ] succ;
  Graphe (int n) { succ = new Liste[n]; }
  ...
  void ajouterArc (int s, int t, int distance) {
    succ[s] = new Liste (
        new Paire (t, distance), succ[s]);
    succ[t] = new Liste (
        new Paire (s, distance), succ[t]);
  }
}

Partie I. Problème en une dimension

Tout se passe en une dimension, et on suppose qu'il faut ouvrir un unique magasin (k = 1). Un site client xi est repéré par son abcisse entière naturelle xi pour tout i (0 £ i < n), et on pose 0 £ xi < xj pour 0 £ i < j < n (On confond, sans ambiguité, site xi et son abscisse xi). Dans un premier temps, on suppose que le coût d'ouverture d'un magasin est le même sur tous les sites. Placer le magasin sur le site xm est un choix optimal si et seulement s'il minimise la quantité S(m) suivante:
S(m) =
n-1
å
i=0
|xi - xm|

Question 1 Calculer xm optimal quand X = {0, 1, 2, 4, 7, 9}.

Question 2 Démontrer que ce minimum est atteint si et seulement si m est en position médiane, c'est-à-dire lorsque le nombre p de xi inférieurs à xm et le nombre q de xi supérieurs à xm vérifient |p - q| £ 1.



A chaque configuration optimale, on associe un mot sur l'alphabet {c, r, m}, obtenu en lisant la succession des points à coordonnées entières sur la ligne, à partir du premier client et jusqu'au dernier client. La lettre c signifie ``client``, m signifie ``magasin``(et un client se trouve également sur ce site), r signifie ``rien``. Dans l'exemple précédent, un mot associé à xm=4 est cccrmrrcrc.

Question 3 Donner le mot associé à xm=2 dans cet exemple.

Question 4 Donner une grammaire algébrique pour engendrer le langage des configurations optimales.

Question 5 Montrer que ce langage n'est pas rationnel (régulier).

On suppose à présent que le coût d'ouverture d'un magasin varie selon le site, et on souhaite choisir le lieu du magasin de façon à minimiser la somme du coût d'ouverture du magasin et de la distance parcourue par les clients. On veut donc minimiser la quantité:
S(m) =
n-1
å
i=0
|xi - xm| + coût(xm)
Remarque: le minimum n'est plus forcément atteint quand m est en position médiane.

Informatiquement, les sites clients sont représentés par un tableau s de n paires s[i] = (xi, ci), trié dans l'ordre croissant des xi, tel que, pour chaque site, la position est en xi et le coût ci d'ouverture d'un magasin sur ce site est coût(xi).

Question 6 Ecrire la fonction magasin1(s) qui prend en argument un tableau de sites s; et qui retourne, en temps linéaire par rapport à n, l'abcisse xm d'un emplacement optimal pour l'ouverture d'un magasin.

Partie II. Allocation de clients à deux magasins de capacité limitée

Dans cette partie, les plus courtes distances entre les sites xi et xj sont données par une matrice symétrique (dij) représentée par un tableau d vérifiant d[i][j] = dij pour tout i, j tels que 0 £ i < n et 0 £ j < n. En outre, il n'y a que deux magasins distincts m et m' dont les emplacements xm et xm' sont donnés. Ces deux magasins ont une capacité limitée à n/2, chaque magasin ne pouvant servir qu'un nombre limité de clients, n/2 au maximum. Pour simplifier, on supposera que n est pair.

On cherche à allouer les clients aux deux magasins en minimisant la somme des distances parcourues par les clients pour se rendre à un magasin, tout en respectant les contraintes de capacité.

Question 7 Montrer qu'une allocation est optimale si et seulement s'il n'existe pas deux clients qui pourraient améliorer la valeur de l'allocation en s'échangeant leurs magasins respectifs.



Dans une classe Tableau, on suppose donnée la méthode trier(a,c) qui trie, en temps O(nlogn), un tableau a de n objets selon la méthode plusPetitQue du comparateur c ordonnant deux objets de a.

  boolean plusPetitQue
    (Object x, Object y);
}
  static void trier
    (Object[ ] a, Comparateur c) {...}
}

Question 8 Définir une classe DeuxMagasins et sa méthode statique allocation(d, m, m') qui prend en arguments le tableau d des distances, les deux magasins m et m'; et qui retourne un tableau de n valeurs valant m ou m' selon que le client situé sur le site xi se rend en xm ou en xm', pour minimiser la somme des distances parcourues par les clients tout en respectant les contraintes de capacités des magasins. Donner sa complexité en temps, par rapport à n.

Partie III. Cas général: placement optimal des magasins

Les sites clients constituent à présent les n sommets d'un graphe G non-orienté dont les arcs sont valués par leurs longueurs. Nous appelons matrice d'adjacence valuée la matrice (mij) telle que mij = l s'il existe, dans G, un arc de longueur l entre le sommet i et le sommet j, et mij = +¥ s'il n'existe pas d'arc entre i et j.

Question 9 Écrire la méthode statique matriceAdjacence(G) qui prend en argument le graphe G; et qui retourne la matrice d'adjacence valuée du graphe G. Donner la complexité en temps de cette fonction.

Question 10 Écrire la méthode statique plusCourtsChemins(G) qui prend en argument le graphe G; et qui retourne la matrice n × n des distances des plus courts chemins entre toute paire de sommets. Donner la complexité en temps de cette fonction.





Le problème général de trouver le placement optimal pour les k magasins sur le graphe G est NP-complet. Pour trouver le meilleur placement, on se contente donc de procéder par énumération sur tous les placements possibles des k magasins sur les sommets du graphe G. Cela revient à énumérer tous les sous-ensembles de taille k de l'ensemble {0, 1, ... n-1}. On codera un tel sous-ensemble par un k-uplet a = á a0, a1, ... ak-1ñ tels qu'on ait a0 < a1 <··· ak-1 et 0 £ ai < n pour 0 £ i < n.

On procède en deux étapes: 1/ définir une classe abstraite générale Enumeration paramétrée par une méthode abstraite action, et écrire, dans cette classe, une méthode iterer qui effectue l'action action(a) pour tout k-uplet a; 2/ considérer une sous-classe de Enumeration qui effectuera les calculs nécessaires pour trouver le placement optimal.



  int[ ] a;
  Enumeration (int k) { a = new int[k]; }
  abstract void action (int[ ] a);
  ...
}

Question 11 Écrire la méthode iterer(k,n) qui appelle la fonction action(a) pour tous les k-uplets a de combinaisons de k nombres parmi n. Quelle est sa complexité en temps?

Question 12 Écrire une méthode statique imprimerCombinaisons(n,k) qui imprime (sans répétitions) toutes les combinaisons de k nombres parmi {0, 1, ... n-1}.



On passe maintenant à la deuxième étape. On suppose qu'un tableau c donne le coût d'ouverture c[i] du magasin situé au sommet i (0 £ i < n).

Question 13 Écrire une fonction valeurDe(d,c,a) qui prend en arguments le tableau des distances d, le tableau c de coûts d'ouverture, et un k-uplet a; et qui retourne la somme S(Y) qui correspond au placement a.

Question 14 En déduire une méthode statique magasins(d,c,k) qui prend en argument le tableau des distances d, le tableau c de coûts d'ouverture, et le nombre k de magasins; et qui retourne le placement optimal á a0, a1, ... ak-1ñ. Quelle est sa complexité en temps?

Partie IV. Placement d'un magasin dans un arbre non-enraciné

Dans cette partie, on suppose qu'il y a un seul magasin à placer (k = 1). Au lieu d'une entreprise de distribution, on envisage une application de type ``construction d'une caserne de pompiers``: le but est de pouvoir rapidement se rendre partout. Ainsi, le placement de la caserne doit maintenant être choisi de façon à minimiser la quantité
M(Y)=max{ d(xi,Y) | xi Î X }
On appelle centre d'un graphe G un sommet y qui minimise M({y}).

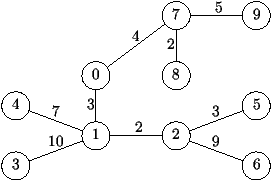
Pour simplifier, on suppose que le graphe non-orienté G a une structure d'arbre non-enraciné: un graphe G est un arbre non-enraciné si, entre toute paire de sommets distincts, il existe un et un seul chemin simple (c'est-à-dire ne passant pas deux fois par le même sommet), comme sur la figure suivante:




On remarque que, dans un arbre non-enraciné, le nombre d'arcs (non-orientés) est égal au nombre de sommets moins un.

Sur la figure, le centre est le sommet 1 dont la distance à tous les autres sommets n'excède pas 12.

Question 15 Donner un algorithme pour trouver, en temps linéaire sur le nombre de sommets n de G, le centre d'un arbre non-enraciné G.
Indications: 1/ on pourra faire deux passes sur le graphe G pour calculer la distance maximale de tout sommet à une feuille; 2/ on suppose qu'on sait calculer b à partir de a de longueur l, en temps O(l), où b est défini par:
b[i] = max{a[j]  |  j ¹ i,  0 £ j < l}     (0 £ i < l)

Question 16 Écrire la méthode statique centre(G) qui prend en argument un arbre non-enraciné G de n sommets; et qui retourne, en temps linéaire par rapport à n, un centre de G.
Indication: on peut utiliser la fonction suivante correspondant à la 2ème indication de la question précédente.
  int ell = a.length; int[ ] b = new int[ell];
  int max = 0, max2 = 0;
  for (int i = 0; i < ell; ++i)
    if (max <= a[i]) {
      max2 = max; max = a[i];
    } else if (max2 < a[i])
      max2 = a[i];
  for (int i = 0; i < ell; ++i)
    if (a[i] == max) b[i] = max2;
    else b[i] = max;
  return b;
}





Corrigé du contrôle classant -- INF 431





Question 1 2 et 4, car S(0) = 1+2+4+7+9 = 23, S(1) = 1+1+3+6+9 = 20, S(2) = 2+1+2+5+7 = 17, S(3) = 4+3+2+3+5 = 17, S(5) = 7+6+5+3+2 = 23, S(6) = 9+8+7+5+2 = 31.

Question 2 
S(i) - S(i-1)
=
i-1
å
j=0
(xi - xj) +
n-1
å
j=i+1
(xj - xi) -
i-2
å
j=0
(xi-1 - xj) -
n-1
å
j=i
(xj - xi-1)
= (xi - xi-1) + (i-1) (xi - xi-1) - (n - i - 1)(xi-1 - xi) - (xi - xi-1)
= (2i - n) (xi - xi-1)

Donc S(i-1) > S(i) si 2i < n; et S(i-1) = S(i) si 2i=n; et S(i-1) < S(i) si 2i > n.

Question 3 ccmrcrrcrc.

Question 4 S ® C S D | m | C m | m D,   C ® c R,   D ® Rc ,   R ® r R | e.

Question 5 On considère le morphisme f tel que f(r) = e. Alors f(L) = {cp m cq | -1 £ p - q £ 1 }. Soit R l'ensemble des mots sur {c, m} de longueur impaire. Si L est rationnel, alors f(L) l'est aussi car image par morphisme. Et comme R est rationnel, on a L Ç R rationnel, puisque les langages rationnels sont clos par intersection. Mais L Ç R = {ci m ci | i ³ 0}. On a vu dans le cours que ce langage ne pouvait être rationnel (lemme de l'étoile). Donc L ne peut être rationnel.

Question 6 Solution en O(n) puisqu'on ne fait qu'un seul parcours de s.

    int n = s.length; int v = s[0].deux;
    for (int i=1; i < n; ++i)
      v = v + s[i].un - s[0].un;
    int iMin = 0; int min = v;
    for (int i=1; i < n; ++i) {
      v = v + (2*i - n) * (s[i].deux - s[i-1].deux) +
        (s[i].un - s[i-1].un);
      if (v < min) { min = v; iMin = i; }
    }
    return s[iMin].un;
  }

Question 7 Le seul sens difficile consiste à montrer que si une allocation n'est pas optimale, alors il existe un échange de deux clients qui améliore S(Y). Si une allocation n'est pas optimale, cela signifie qu'on peut changer l'allocation d'un sous-ensemble de X entre xm et xm'. Autrement dit, pour Z = {xi1, ... xil} et Z' = {x'i1, ... x'il}, on a:
 
å
xi Î Z
d(xi, xm) +
 
å
x'i Î Z'
d(x'i, xm') >
 
å
xi Î Z
d(xi, xm') +
 
å
x'i Î Z'
d(x'i, xm)
En posant d(x) = d(x, xm) - d(x, xm'), cela revient à dire
E =
 
å
xi Î Z
d(xi) -
 
å
x'i Î Z'
d(x'i) > 0
Or un échange entre x et x' baisse la valeur de S(Y) ssi d(x) > d(x'). Donc s'il n'existe aucun échange possible entre X et X' pour diminuer S(Y), on a E £ 0 et une contradiction.

Question 8 

  Paire[ ] delta;

  DeuxMagasins (int[ ][ ] d, int m1, int m2) {
    int n = d[0].length;
    Paire[ ] delta = new Paire[n];
    for (int i=0; i < n; ++i) {
      delta[i].un = d[i][m1] - d[i][m2];
      delta[i].deux = i;
    }
  }

  public boolean plusPetitQue (Object x, Object y) {
    return ((Paire)x).un <= ((Paire)y).un;
  }

  static int[ ] allocation (int[ ][ ] d, int m1, int m2) {
    DeuxMagasins mm = new DeuxMagasins (d, m1, m2);
    Tableau.trier (mm.delta, mm);
    int n = d[0].length;
    int[ ] r = new int[n];
    for (int i=0; i < n/2; ++i) r[mm.delta[i].deux] = m1;
    for (int i=n/2; i < n; ++i) r[mm.delta[i].deux] = m2;
    return r;
  }
}

Question 9 La construction de la matrice parcourt les sommets et tous les arcs en O(n+E), donc O(n2) avec l'initialisation de d.

    int n = g.succ.length;
    int[ ][ ] d = new int[n][n];
    for (int x = 0; x < n; ++x)
      for (int y = 0; y < n; ++y)
        d[x][y] = Integer.MAX_VALUE;
    for (int x = 0; x < n; ++x)
      for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
          int y = ls.val.un; int dxy = ls.val.deux;
          d[x][y] = dxy;
      }
    return d;
  }

Question 10 Algorithme de Floyd-Warshall en O(n3) vu dans le cours.

    int n = g.succ.length;
    int[ ][ ] d = matriceAdjacence (g);
    for (int k = 0; k < n; ++k)
      for (int x = 0; x < n; ++x)
        for (int y = 0; y < n; ++y)
          d[x][y] = Math.min (d[x][y], d[x][k] + d[k][y]);
    return d;
  }

Question 11 


  void iterer1 (int k, int i, int n) {
    if (k == 0) action (a);
    else {
      int k0 = a.length;
      for (int j = i; j < n; ++j) {
        a[k0-k] = j;
        iterer1 (k-1, j+1, n);
  } } }

Question 12 

  Impression (int k) { super(k); }

  void action (int[ ] a) {
    for (int i = 0; i < a.length; ++i)
      System.out.print (a[i] + " ");
    System.out.println();
} }

  static void imprimer (int n, int k) {
    Impression imp = new Impression(k);
    imp.iterer(k, n);
  }

Question 13 

    int n = d[0].length, k = a.length;
    int v = 0;
    for (int j = 0; j < k; ++j) v = v + c[j];
    for (int i = 0; i < n; ++i)
      v = v + distMagasinLePlusProche (d, i, a);
    return v;
  }

  static int distMagasinLePlusProche (int[ ][ ] d, int i, int[ ] a) {
    int k = a.length;
    int v = Integer.MAX_VALUE;
    for (int j = 0; j < k; ++j)
      v = Math.min (v, d[i][a[j]]);
    return v;
  }

Question 14 

  int vMin = Integer.MAX_VALUE; int[ ] r; int[ ][ ] d;
  Affectation (int k, int[ ][ ] d0) {
    super(k); r = new int[k]; d = d0;
  }

  void action (int[ ] a) {
    int v = valeurDe (d, c, a);
    if (v < vMin)
      for (int i = 0; i < a.length; ++i)
        r[i] = a[i];
  }
}

  static int[ ] magasins (int[ ][ ] d, int[ ] c, int k) {
    int n = d[0].length;
    Affectation f = new Affectation(k, d, c);
    f.iterer(k, n);
    return f.r;
  }

Question 15 Dans une première passe, on fait un parcours dfs produisant un arbre de recouvrement A en calculant les hauteurs internes (valuées) h(x) des noeuds x de A, c'est-à-dire les plus longues distances des chemins à des feuilles en ne passant que par des noeuds internes au sous-arbre de racine x.
h(x) = max{d(x,y)+h(y) | y sous-arbre de x dans A }
Dans une deuxième passe, en faisant le même parcours dfs, on calcule les hauteurs externes des noeuds y, c'est-à-dire les plus longues distances des chemins à des feuilles en ne passant que par des sommets extérieurs au sous-arbre de racine y.
he(y) = d(y,x) + max({he(x)} È {d(x,z)+h(z) | z frère de y dans A })
où x est le père de y. Le plus long chemin issu de x est donc max{h(x), he(x)}. Le centre de G est obtenu en cherchant le minimum de cette valeur sur tous les sommets de G.

Question 16 


  static int[ ] hauteur (Graphe g) {
    int n = g.succ.length; int[ ] couleur = new int[n];
    int[ ] r = new int[n];
    for (int x = 0; x < n; ++x) couleur[x] = BLANC;
    hauteur1(g, r, 0, couleur);
    return r;
  }

  static void hauteur1 (Graphe g, int[ ] r, int x, int[ ] couleur) {
    couleur[x] = GRIS; int h = 0;
    for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
      int y = ls.val.un; int dxy = ls.val.deux;
      if (couleur[y] == BLANC) {
        hauteur1(g, r, y, couleur);
        h = Math.max(h, dxy + r[y]);
      }
    }
    r[x] = h;
  }

  static int[ ] exterieur (Graphe g, int[ ] h) {
    int n = g.succ.length; int[ ] couleur = new int[n];
    int[ ] r = new int[n];
    for (int x = 0; x < n; ++x) couleur[x] = BLANC;
    exterieur1(g, h, r, 0, couleur);
    return r;
  }

  static void exterieur1 (Graphe g, int[ ] h, int[ ] r, int x, int[ ] couleur) {
    couleur[x] = GRIS;
    int ell = Liste.longueur(g.succ[x]);
    int[ ] a = new int[ell+1];
    a[0] = r[x]; int i = 1;
    for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
      int y = ls.val.un; int dxy = ls.val.deux;
      a[i++] = dxy + h[y];
    }
    int[ ] b = maxExterne(a); int j = 1;
    for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
      int y = ls.val.un; int dxy = ls.val.deux;
      if (couleur[y] == BLANC) {
        r[y] = dxy + b[j++];
        exterieur1 (g, h, r, y, couleur);
      }
    }
  }

  static int centre (Graphe g) {
    int n = g.succ.length;
    int[ ] h = hauteur(g), he = exterieur(g, h);
    int m = Integer.MAX_VALUE; int iMin = -1;
    for (int x = 0; x < n; ++x)
      if (Math.max (h[x], he[x]) < m) {
        iMin = x; m = Math.max(h[x], he[x]);
      }
    return iMin;
  }

1

avec les participations de Robert Cori et Frédéric Magniez
This document was translated from LATEX by HEVEA.