Contrôle hors-classement
École polytechnique
Informatique -- Cours INF 431
Frédéric Magniez et Jean-Jacques Lévy
12 avril 2005 |
Attention: On attachera une grande importance à la clarté, à la
précision et à la concision de la rédaction. Le sujet étant trop long,
la 4ème partie est optionnelle.
La compagnie d'électricité veut distribuer l'électricité dans un
nouveau territoire en minimisant la quantité de cable à tirer entre
les emplacements des sources d'énergie et des différents clients à
desservir.
| 1 |
Modélisation du problème |
|
On modélise ce problème en considérant un graphe non-orienté et valué
G = (V, E, d). Les emplacements des centrales et des clients
constituent les sommets V de ce graphe G; les cables à tirer entre
deux sommets proches en sont les arcs a, avec une longueur associée
d(a) (d(a) > 0) comme sur la figure 1a. On
suppose le graphe G connexe.
 |
|
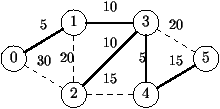 |
| (a) |
|
(b) |
Figure 1: (a) Graphe non-orienté et valué; (b) Arbre de recouvrement minimal.
Le problème consiste à trouver un arbre de recouvrement minimal pour
G, c'est-à-dire un arbre de recouvrement dont la somme des longueurs
de ses branches est minimale.
L'algorithme glouton de Prim construit progressivement l'arbre de
recouvrement minimal en partant d'un sommet arbitraire, et en
ajoutant, à tout moment, un arc de longueur minimale vers un sommet
qui n'appartient pas encore à l'arbre de recouvrement. Quand on a
atteint tous les sommets du graphe, l'algorithme se termine (cf. la
figure 1b).
Question
1 Montrer les différentes étapes de construction
d'un arbre de recouvrement minimal à partir du sommet 0 sur
le graphe de la figure 1a.
Question
2 Montrer que si on considère une partition des sommets du
graphe G en deux sous-ensembles disjoints X et V-X, tout arbre de
recouvrement minimal contient forcément un arc de longueur minimal
reliant un sommet de X et un sommet de V-X.
(Indication: montrer
que, si ce n'est pas le cas, on peut remplacer un des arcs de l'arbre
de recouvrement reliant ces deux sous-ensembles par un arc de longueur
plus petite les reliant.)
Question
3 Montrer que l'algorithme de Prim trouve un arbre de
recouvrement minimal.
| 2 |
Représentation des données |
|
Les arcs sont représentés par des objets avec trois champs:
org pour désigner le sommet origine de l'arc,
dst pour son sommet destination, longueur pour
sa longueur. Dans le graphe non-orienté G, s'il existe un arc a de
x à y, il existe aussi un arc b de y à x de même longueur.
Le graphe G est représenté par un tableau de successeurs; plus
exactement, la liste succ[x] est la liste des
arcs dont l'origine est x.
On a donc les classes suivantes:
|
class Arc {
int org, dst, longueur;
Arc (int x, int y, int w) {
org = x; dst = y; longueur = w;
} } |
|
class Liste {
Arc val; Liste suivant;
Liste (Arc a, Liste ls) {
val = a; suivant = ls;
} } |
|
class Graphe {
Liste succ[ ];
...
}
|
L'arbre de recouvrement minimal se construit progressivement en
maintenant sa frontière f, c'est-à-dire un ensemble d'arcs
dont l'origine est dans l'arbre de recouvrement et la destination
n'est pas dans l'arbre de recouvrement. En outre, on s'arrange pour
que, pour toute paire d'arcs distincts a et b dans f, les
destinations sont aussi distinctes. Cette frontière est représentée
par la classe suivante:
abstract class Frontiere {
abstract void ajouter (Arc a);
abstract void majAvec (Arc a);
abstract Arc extraireMin();
}
La classe Frontiere contient deux méthodes:
ajouter(a) pour ajouter un nouvel arc a dans la
frontière; extraireMin() qui retourne et supprime l'arc
a de longueur minimum dans la frontière. Une troisième méthode
majAvec(a) met à jour dans f l'arc b de même
destination que celle de a, en ne gardant, dans f, que celui de
a ou de b qui a la plus petite longueur.
On considère une sous-classe FrontiereSeq qui implémente
la frontière en la représentant par la liste á a1, a2, ...
ak ñ des arcs qu'elle contient. Le champ elts de
FrontiereSeq désigne cette liste. Pour accélérer,
l'opération de mise à jour, un autre champ pos est un
tableau qui donne, pour tout sommet x du graphe G, la position,
dans cette liste, de l'arc a dont la destination est x. On a donc
pos[x] = á a, ai+1, ai+2 ... ak ñ.
(Cette optimisation est facultative.)
A présent, on écrit les différentes méthodes manipulant la frontière:
Question
4 Définir cette classe FrontiereSeq qui implémente
la classe Frontiere. Donner son constructeur
FrontiereSeq(n) en supposant que le graphe contient n
sommets (n > 0).
Question
5 Écrire la méthode ajouter(a) qui ajoute l'arc
a à la frontière. (On suppose que le sommet destination de a n'est
pas la destination d'un autre arc b déjà présent dans la frontière) Quelle
est la complexité en temps de cette fonction?
Question
6 Écrire la méthode majAvec(a) qui met à jour la
frontière avec l'arc a. (On suppose que le sommet destination de a
est la destination d'un autre arc b présent dans la frontière)
Quelle est la complexité en temps de cette fonction?
Question
7 Écrire la méthode extraireMin() qui retourne
l'arc de longueur minimale dans la frontière et l'enlève de la
frontière. Quelle est la complexité en temps de cette fonction?
L'arbre de recouvrement minimal est représenté par un tableau p[ ]
tel que p[y] = x si le sommet x est le père de y dans l'arbre de
recouvrement (0 £ y < n). Pour la racine r, on pose p[r] =
-1.
Question
8 Écrire la fonction statique mst(G) dans la
classe Graphe qui retourne un arbre de recouvrement
minimal de G. Quelle est la complexité en temps de cette fonction?
Question
9 Comment représenter la frontière pour améliorer la complexité
en temps de mst ?
Question
10 Comment modifier mst(G) pour obtenir une
forêt de recouvrement minimale quand G n'est pas connexe?
| 4 |
Programmation par objets |
|
La direction informatique de la compagnie d'électricité exige ``un
style de programmation plus moderne``, c'est-à-dire une programmation
par objets. Nous changeons donc la représentation des ensembles d'arcs
en utilisant un type disjonctif distinguant la classe Vide
pour représenter l'ensemble vide et la classe NonVide pour
représenter des ensembles non vides. Ces deux classes sont des
sous-classes de la classe des ensembles d'arcs suivante:
abstract class Ensemble {
abstract Ensemble ajouter (Arc a);
abstract Ensemble enlever (Arc a);
abstract Arc minimum();
}
où l'expression e.ajouter(a) ajoute l'arc
a à l'ensemble e; où e.enlever(a) retire l'arc a
de l'ensemble e; et où e.minimum() retourne un arc de
longueur minimale appartenant à l'ensemble e.
La frontière est à présent représentée par une sous-classe
FrontiereSeqEns de Frontiere, qui utilise
les méthodes de la classe Ensemble.
Question
11 Écrire les méthodes des classes Vide,
NonVide et FrontiereSeqEns permettant de gérer
la frontière comme dans la classe FrontiereSeq.
Question
1
Question
2 Remarquons d'abord les deux points suivants. Soient T un
arbre de recouvrement de G et a un arc de G qui n'est pas dans
T. Si a est ajouté à T, le graphe T' obtenu contient un
unique cycle C., Deuxièmement, si un arc quelconque du cycle C est
supprimé dans T', le graphe obtenu T'' est à nouveau un graphe de
recouvrement.
Appelons mst un arbre de recouvrement minimal de G.
Soit M un mst de G ne contenant pas d'arc a de longueur minimale entre
X et V-X.
Appliquons les deux remarques préliminaires. Si a est ajouté à M,
un cycle est créé. Ce cycle contient un autre arc b reliant X et
V-X. En supprimant b, un nouvel arbre de recouvrement est créé,
dont la somme des longueurs est plus petite : contradiction.
Question
3 Lorsque les longueurs des arcs ne sont pas toutes deux à
deux distinctes, nous avons besoin du résultat suivant du même type
que celui de la question précédente.
Soit S l'ensemble des arcs de longueur minimale reliant un sommet de
X et un sommet de V-X. Alors, tout mst M peut être modifié en
ajoutant arbitrairement un arc de S-M et en supprimant un arc de
MÇ S bien choisi.
Pour le voir, il suffit d'appliquer la méthode précédente. En
ajoutant un arc a de S-M un cycle est créé. Pour le défaire on
enlève un autre arc b du cycle entre X et V-X. La longueur de
b est nécessairement plus grande ou égale à celle de a. Mais
puisque M était déjà de longueur minimale, nécessairement les arcs
a et b sont de même longueur. Le nouvel arbre de recouvrement a
la même longueur que M qui est donc toujours minimale.
Nous allons prouver par induction que l'arbre Mk, obtenu à l'étape
k de l'algorithme de Prim, est un préfixe d'un mst de G, pour
k=0,1,...,n.
Soit Xk l'ensemble des k sommets de Mk.
Pour k=0, l'abre M0 a un seul noeud x, donc il est préfixe
de tout mst (contenant forcément x).
Supposons par récurrence, que Mk est le préfixe d'un mst M de
G. L'arbre M étant un mst, il contient forcément un arc a de
longueur minimale entre entre Xk et V-Xk. S'il n'y a qu'un seul
arc de longueur minimale entre Xk et V-Xk, il s'agit de a, et
l'algorithme le trouve et le rajoute à Mk pour former Mk+1 qui
est un préfixe de M, et qui satisfait donc l'hypothèse de
récurrence. En cas d'ambiguité, l'algorithme ajoutera un arc b de
même longueur que a, obtenant ainsi Mk+1. Si b est dans M,
on est dans le cas précédent. Sinon, d'après le résultat énoncé en
début de question, il est possible de remplacer un arc de M qui est
entre Xk et V-Xk par b de telle sorte que l'arbre obtenu M'
est toujours un mst. Comme l'arc retiré de M n'était pas dans
Mk, l'arbre Mk+1 est bien préfixe du mst M'
La récurrence est donc finie. Quand k=n, l'arbre Mk est donc un
mst de G.
Question
4
class FrontiereSeq extends Frontiere {
Liste elts;
Liste[ ] pos;
FrontiereSeq (int n) { elts = null ; pos = new Liste[n]; }
...
}
Question
5 La fonction a une complexité O(1).
void ajouter (Arc a) {
elts = new Liste (a, elts);
pos[a.dst] = elts;
}
Question
6 La fonction a une complexité O(1).
void majAvec (Arc a) {
Liste ls = pos[a.dst];
if (a.longueur < ls.val.longueur)
ls.val = a;
}
Question
7 La fonction suivante prend un temps O(k) si k arcs dans f.
void supprimer (Arc a) {
elts = enleverArcDans (a, elts);
pos[a.dst] = null;
}
Liste enleverArcDans (Arc a, Liste ls) {
if (ls != null) {
if (ls.val == a) ls = ls.suivant;
else ls.suivant = enleverArcDans (a, ls.suivant);
}
return ls;
}
Arc minimum() {
if (elts == null) return null;
else {
Arc aMin = elts.val;
for(Liste ls = elts.suivant; ls != null; ls = ls.suivant)
if (ls.val.longueur < aMin.longueur) aMin = ls.val;
return aMin;
}
}
Arc extraireMin() {
Arc a = minimum();
supprimer (a);
return a;
}
Question
8 La fonction suivante a une complexité en O(V2) + O(E),
c'est-à-dire O(V2) = O(n2).
final static int BLANC = 0, GRIS = 1, NOIR = 2;
static int[ ] mst (Graphe g) {
int n = g.succ.length;
int[ ] pere = new int[n];
int[ ] couleur = new int[n];
for(int i = 0; i < n; ++i) {
couleur[i] = BLANC; pere[i] = -1;
}
Frontiere f = new FrontiereSeq(n);
f.ajouter (new Arc(-1, 0, 0));
for(int i = 0; i < n; ++i) {
Arc a = f.extraireMin();
int x = a.dst;
pere[x] = a.org; couleur[x] = NOIR;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
Arc b = ls.val; int y = b.dst; // b ARC DE x A y
if (couleur[y] == BLANC) {
couleur[y] = GRIS;
f.ajouter(b);
}
else if (couleur[y] == GRIS)
f.majAvec(b);
}
}
return pere;
}
Question
9 On peut utiliser une file de priorité de type tas de sable, et réduire les temps
d'extraction du minimum à O(logk),
où k est le nombre d'arcs dans la frontière.
Par contre, les temps de mise à jour et d'ajout passent alors de O(1) à O(logk).
D'où un mst en O((E + V) logV).
Remarque : en utilisant des tas de Fibonacci, il serait possible de dessendre les temps
de mise à jour et d'ajout à O(1) ce qui donnerait alors O(E+ VlogV).
Question
10 Il suffit de changer la condition d'arrêt de mst.
for (int x = 0; x < n; ++x) {
if (couleur[i] == BLANC) {
Frontiere f = new FrontiereSeq(n);
f.ajouter (new Arc(-1, x, 0));
Arc a; while ((a = f.extraireMin()) != null) {
int x = a.dst;
...
} } }
Question
11
class Vide extends Ensemble {
Ensemble ajouter (Arc a) {return new NonVide (a, this); }
Ensemble enlever (Arc a) {return this; }
Arc minimum() { return null; }
}
class NonVide extends Ensemble {
Arc elt; Ensemble reste;
NonVide (Arc a, Ensemble e) { elt = a; reste = e; }
Ensemble ajouter (Arc a) {return new NonVide (a, this); }
Ensemble enlever (Arc a) {
if (elt == a) return reste;
else {reste = reste.enlever (a); return this; }
}
Arc minimum () {
Arc b = reste.minimum();
if (b == null || elt.longueur <= b.longueur) return elt;
else return b;
}
}
class FrontiereSeqEns extends Frontiere {
Ensemble arcs;
Ensemble[ ] pos;
FrontiereSeqEns (int n) {
arcs = new Vide() ; pos = new Ensemble[n];
}
void ajouter (Arc a) {
arcs = arcs.ajouter (a);
pos[a.dst] = arcs;
}
void majAvec (Arc a) {
NonVide e = (NonVide) pos[a.dst];
if (a.longueur < e.elt.longueur)
e.elt = a;
}
void supprimer (Arc a) {
arcs = arcs.enlever (a);
pos[a.dst] = null;
}
Arc extraireMin() {
Arc a = arcs.minimum();
supprimer (a);
return a;
}
This document was translated from LATEX by
HEVEA.



