


L es graphes sont des structures combinatoires rencontrées
dans des applications faisant intervenir des mathématiques discrètes
et nécessitant une solution informatique. Circuits électriques,
réseaux de transport (ferrés, routiers, aériens), réseaux
d'ordinateurs, ordonnancement d'un ensemble de tâches sont les
principaux domaines d'application où la structure de graphe
intervient. D'un point de vue formel, il s'agit d'un ensemble de
points (sommets) et d'un ensemble d'arcs reliants des couples de
sommets. Une des premières questions que l'on se pose est de
déterminer, étant donné un graphe et deux de ses sommets, s'il existe
un chemin (suite d'arcs) qui les relie; cette question très simple
d'un point de vue mathématique pose des problèmes d'efficacité dès que
l'on souhaite la traiter à l'aide de l'ordinateur pour des graphes
comportant un très grand nombre de sommets et d'arcs. Pour se
convaincre de la difficulté du problème il suffit de considérer le jeu
d'échecs et représenter chaque configuration de pièces sur l'échiquier
comme un sommet d'un graphe, les arcs joignent chaque configuration à
celles obtenues par un mouvement d'une seule pièce; la résolution d'un
problème d'échecs revient ainsi à trouver un ensemble de chemins
menant d'un sommet à des configurations de ``mat ``. La
difficulté du jeu d'échecs provient donc de la quantité importante de
sommets du graphe que l'on doit parcourir. Des graphes plus simples
comme celui des stations du Métro Parisien donnent lieu à des
problèmes de parcours beaucoup plus facilement solubles.
Il est courant,
lorsque l'on étudie les graphes, de distinguer entre les graphes
orientés dans lesquels les arcs doivent être parcourus dans un sens
déterminé (de x vers y mais pas de y vers x) et les graphes
symétriques (ou non-orientés) dans lesquels les arcs (appelés alors
arêtes) peuvent être parcourus dans les deux sens. Nous nous limitons
dans ce chapitre aux graphes orientés, car les algorithmes de parcours
pour les graphes orientés s'appliquent en particulier aux graphes
symétriques : il suffit de construire à partir d'un graphe symétrique
G le graphe orienté G' comportant pour chaque arête x,y de G
deux arcs opposés, l'un de x vers y et l'autre de y vers x.
Dans ce paragraphe, nous donnons quelques définitions sur les graphes
orientés et quelques exemples, nous nous limitons ici aux définitions
les plus utiles de façon à passer très vite aux algorithmes.
Définition 1
Un graphe G = (X,A) est donné par un ensemble X de sommets et par un sous-ensemble A du produit cartésien X ×
X appelé l'ensemble des arcs de G.
Un arc a=(x,y) a pour origine le sommet x et pour extrémité le sommet y. On note
org(a) = x ext(a) = y
Dans la suite, on suppose que tous les graphes considérés sont finis,
ainsi X et par conséquent A sont des ensembles finis. On dit que
le sommet y est un successeur de x si (x,y) Î A, on dit
aussi que x est un prédécesseur de y.
Définition 2 Un chemin f du graphe G=(X,A) est une suite
d'arcs á a1,a2,...,apñ telle que:
" i, 1 £ i< p org(ai+1) = ext(ai)
L'origine d'un chemin f, aussi notée org(f), est celle de
son premier arc a1 et son extrémité, notée ext(f) est
celle de son dernier arc ap. La longueur du chemin est égale
au nombre d'arcs qui le composent, c'est-à-dire p. Un chemin f tel
que org(f)=ext(f) est appelé un circuit.
Exemple 1 Graphes de De Bruijn.
Les sommets sont les suites de longueur k formées de symboles
0 ou 1, un arc joint la suite f à la suite g si f=xh et
g=hy où x et y sont des symboles (0 ou 1) et où h est une
suite quelconque de k-1 symboles.
Figure 1.1 : Graphe de De Bruijn pour k=3; graphe des diviseurs pour n=12
Exemple 2 Graphes des diviseurs.
Les sommets sont les nombres {2,3,..., n}, un arc joint p à
q si p divise q.
Une structure de données simple pour représenter un graphe est la
matrice d'adjacence M. Pour obtenir M, on numérote les sommets
du graphe de façon quelconque:
X= {x1, x2... xn }
M est une matrice booléenne carrée n × n dont les
coefficients sont V et F telle que:
Ceci donne alors les déclarations de type et de variables
suivantes:
class GrapheMat {
boolean[ ][ ] m; // la matrice M d'adjacence,
GrapheMat (int n) {
m = new boolean[n][n];
}
} |
|
|
| M = |
æ
ç
ç
ç
ç
ç
ç
è |
| F |
V |
V |
F |
F |
F |
| F |
F |
V |
V |
F |
V |
| F |
F |
F |
F |
F |
V |
| F |
F |
F |
F |
V |
F |
| F |
V |
F |
F |
F |
F |
| F |
F |
F |
V |
F |
F |
|
|
ö
÷
÷
÷
÷
÷
÷
ø |
|
|
Figure 1.2 : Un graphe avec sa matrice d'adjacence
La matrice d'adjacence aurait aussi pu être représentée
par une matrice d'entiers (0 pour F, 1 pour V). Un intérêt de
cette autre représentation est que la détermination de chemins dans G
revient au calcul des puissances successives de la matrice M comme
le montre le théorème suivant.
Théorème 3
Soit Mp la puissance p-ième de la matrice M, le coefficient
Mi,jp est égal au nombre de chemins de longueur p de G
dont l'origine est le sommet xi et dont l'extrémité est le
sommet xj.
Démonstration Par récurrence sur p. Pour p=1, le résultat est
immédiat car un chemin de longueur 1 est un arc du graphe. Pour p >
1, le calcul de Mp donne:
Or tout chemin de longueur p entre xi et xj se décompose en un
chemin de longueur p-1 entre xi et un certain xk suivi d'un
arc reliant xk et xj. Le résultat découle alors de l' hypothèse
de récurrence suivant laquelle Mi,kp-1 est le nombre de
chemins de longueur p-1 joignant xi à xk.
De ce théorème, on déduit l'algorithme suivant permettant de
tester l'existence d'un chemin entre deux sommets x et y:
static boolean existeChemin (GrapheMat g, int x, int y) {
int n = g.m.length;
boolean r[ ][ ] = new boolean[n][n];
copie(r, m);
for (int p = 1; !r[x][y] && p < n; ++p) {
multiplier (r, r, m);
additionner (r, r, m);
}
return r[x][y];
} |
Les fonctions multiplier(r,a,b) et additionner(r,a,b) sont
respectivement des fonctions qui multiplient et ajoutent les deux
matrices booléennes a et b (de dimension n × n) en rangeant
le résultat dans la matrice r. La fonction copie(r,m) fait
une copie de m dans la matrice r.
Le nombre d'opérations effectuées par l'algorithme est de l'ordre de
n4, car le produit de deux matrices carrées n × n demande
n3 opérations et l'on peut avoir à effectuer n produits de
matrices. La recherche du meilleur algorithme possible pour le calcul
du produit de deux matrices a été très intense ces dernières années.
Plusieurs améliorations de l'algorithme élémentaire demandant n3
multiplications ont été successivement trouvées. Coppersmith et
Winograd détiennent le record avec un algorithme en O(n2.5); mais
ce résultat reste très théorique, car la programmation de leur
algorithme n'est pas aisée et l'efficacité espérée n'est atteinte que
pour de très grandes valeurs de n. On cherche donc à construire
d'autres algorithmes, faisant intervenir des notions différentes.
Enfin, notons que, si on se limite à la recherche de l'existence d'un
chemin entre deux sommets x et y donnés, on peut ne calculer
qu'une seule ligne de la matrice, ce qui diminue notablement la
complexité.
La fonction existeChemin, vue précédemment, ne fait rien de plus
qu'un calcul naïf de la notion suivante:
la fermeture transitive d'un graphe G=(X,A) est la relation binaire
transitive minimale contenant la relation A sur X. Il s'agit d'un
graphe G*=(X,A*) tel que (x,y) Î A* si et seulement s'il
existe un chemin f dans G d'origine x et d'extrémité y.
Figure 1.3 : Un graphe et sa fermeture transitive
Le calcul de la fermeture transitive permet donc de répondre aux
questions concernant l'existence de chemins entre tout couple de
sommets x et y dans G. On effectue un pré-traitement de
G en calculant G*=(X,A); puis on répond en temps constant,
O(1), à toute question sur l'existence de chemins entre x et y.
Une autre application du calcul de la fermeture transitive est
fréquente en compilation: un graphe est associé à chaque fonction d'un
programme, les sommets de ce graphe représentent les variables de la
fonction et un arc entre la variable a et la variable b indique
que le calcul de la valeur a fait appel au calcul de la valeur de
b. La fermeture transitive de ce graphe de dépendances
donne alors toutes les variables intervenant dans le calcul de a.
Le calcul de (X,A*) s'effectue par itération de l'opération de
base Fx(A) qui ajoute à A les arcs (y,z) tels que y est
un prédécesseur de x et z un de ses successeurs. Posons:
Fx(A) = A È { (y,z) | (y,x) Î A, (x,z) Î A }
Cette opération satisfait les deux propriétés suivantes:
Figure 1.4 : L'effet de l'opération Fx: les arcs ajoutés sont en pointillé
Proposition 4
Pour tout sommet x, on a
Fx(Fx(A))=Fx(A)
et pour tout couple de sommets (x,y) :
Fx(Fy(A))=Fy(Fx(A))
Démonstration La première partie est très simple, on l'obtient en
remarquant que (u,x) Î Fx(A) implique (u,x) Î A et que
(x,v) Î Fx(A) implique (x,v) Î A .
Pour la seconde partie, il suffit de vérifier que si (u,v)
appartient à Fx(Fy(A)) il appartient aussi à
Fy(Fx(A)). Le résultat s'obtient ensuite par symétrie. Si
(u,v) Î Fx(Fy(A)), alors ou bien (u,v) Î Fy(A), ou
bien (u,x) et (x,v) Î Fy(A). Dans le premier cas,
Fy(A') É Fy(A) pour tout A' É A implique
(u,v) Î Fy(Fx(A)). Dans le second cas, il y a plusieurs
situations à considérer suivant que (u,x) ou (x,v) appartiennent
ou non à A; l'examen de chacune d'entre elles permet d'obtenir le
résultat. Examinons en une à titre d'exemple, supposons que (u,x) Î
A et (x,v) Ï A. Comme (x,v) Î Fy(A), on a (x,y)Î A
et (y,v) Î A. Ceci implique (u,y) Î Fx (A) et (u,v) Î
Fy(Fx(A)).
Proposition 5
La fermeture transitive A* est donnée par :
A* = Fx1( Fx2( ... Fxn(A)... ))
Démonstration On se convainc facilement que A* contient
l'itérée de l'action des Fxi sur A, la partie la plus
complexe à prouver est que Fx1( Fx2( ...
Fxn(A)... )) contient A*. Pour cela on considère un
chemin joignant deux sommets x et y de G alors ce chemin
s'écrit (x,y1)(y1,y2)... (yp,y)
ainsi (x,y) Î
Fy1( Fy2( ... Fyp(A)... )) les
propriétés démontrées ci-dessus permettent d'ordonner les y
suivant leurs numéros croissants; le fait que Fy(A') É
A', pour tout A' permet ensuite de conclure.
De ces deux résultats, on obtient l'algorithme de Roy et Warshall
suivant pour le calcul de la fermeture transitive d'un graphe:
static void phi (GrapheMat g, int x) {
int n = g.m.length;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
g.m[i][j] = g.m[i][j] || g.m[i][x] && g.m[x][j];
}
static public void fermetureTransitive (GrapheMat g) {
for (int k = 0; k < g.m.length; ++k)
phi(g, k);
} |
Dans la fonction phi, la matrice est modifiée en cours de
calcul; grâce à la proposition 4, cela ne change
pas le résultat final puisque Fx = Fx2. Maintenant, si on
déplie l'appel de la fonction phi (inlining en anglais),
on obtient:
static public void fermetureTransitive (GrapheMat g) {
int n = g.m.length;
for (int k = 0; k < n; ++k)
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
g.m[i][j] = g.m[i][j] || g.m[i][k] && g.m[k][j];
} |
Cette fonction modifie le graphe G. Une bien meilleure
solution consiste à donner comme résultat un nouveau graphe G* de
la manière suivante:
static public GrapheMat fermetureTransitive (GrapheMat g) {
GrapheMat r = copieGraphe (g);
int n = g.m.length;
for (int k = 0; k < n; ++k)
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
r.m[i][j] = r.m[i][j] || r.m[i][k] && r.m[k][j];
return r;
}
GrapheMat copieGraphe (GrapheMat g) {
int n = g.m.length;
GrapheMat r = new GrapheMat (n);
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
r.m[i][j] = g.m[i][j];
return r;
} |
L'algorithme ci-dessus effectue un nombre d'opérations que
l'on peut majorer par n3, chaque exécution de la fonction
phi pouvant nécessiter n2 opérations; cet algorithme est
donc meilleur que le calcul des puissances successives de la matrice
d'adjacence.
Finalement, on remarquera que la fermeture transitive calculée dans
cette section ne contient pas la relation identité. Elle ne contient
pas les chemins de longueur nulle joignant tout sommet x à lui-même.
Pour calculer cette fermeture transitive au sens large, on modifie
très simplement l'algorithme de Warshall en ajoutant la matrice
identité au résultat.
| 1.4 |
Listes de successeurs |
|
La matrice d'adjacence peut être très creuse, une façon plus compacte
de représenter un graphe consiste à associer à chaque sommet x la
liste de ses successeurs. On utilise un tableau de listes que l'on
note succ; on suppose que les sommets sont numérotés de 0 à
n-1; la quantité succ[x] désigne la liste des successeurs de
x. Cette représentation est utile pour obtenir tous les successeurs
d'un sommet x. Elle permet leur accès en un nombre d'opérations égal
au nombre d'éléments de cet ensemble et non pas au nombre total de
sommets comme c'est le cas dans la matrice d'adjacence, ce qui peut
faire une différence sensible quand n est grand. Pour un graphe
G=(X,A), la place prise en mémoire est en O(|X|+|A|) au lieu
d'être en O(|X|2) pour la représentation matricielle. Dans le cas
du graphe de la figure 1.2, la représentation se trouve à
présent sur la figure 1.5.
Une nouvelle classe Graphe correspond à la représentation par
listes de successeurs:
|
|
|
|
|
|
|
succ[0] |
|
= |
|
á 1, 2ñ |
|
succ[1] |
|
= |
|
á 3, 2, 5ñ |
|
succ[2] |
|
= |
|
á 5ñ |
|
succ[3] |
|
= |
|
á 4ñ |
|
succ[4] |
|
= |
|
á 1ñ |
|
succ[5] |
|
= |
|
á 3ñ |
|
|
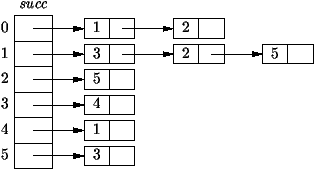 |
Figure 1.5 : Représentation des graphes par listes de successeurs
class Graphe {
Liste[ ] succ;
Graphe (int n) { succ = new int[n]; }
}
class Liste {
int val;
Liste suivant;
Liste (int x, Liste ls) { val = x; suivant = ls; }
} |
La déclaration de la classe Liste est la définition classique des
listes d'entiers. Le parcours de la liste des successeurs y
d'un sommet x s'effectue à l'aide de la suite des instructions
suivantes. On retrouvera cette suite d'instructions comme brique de
base de beaucoup de constructions d'algorithmes sur les graphes:
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
Traitement de y
} |
que l'on peut résumer en langue naturelle de la manière suivante:
Pour tout sommet y, successeur du sommet x dans G, faire {
Traitement de y
} |
On peut passer de la représentation d'un graphe par une matrice
d'adjacence à la représentation par listes de successeurs en définissant
dans la classe Graphe le constructeur suivant:
Graphe (GrapheMat g) {
int n = g.m.length;
succ = new Liste[n];
for (int i = 0; i < n; ++i) {
for (int j = n-1; j >= 0; --j)
if (g.m[i][j])
succ[i] = new Liste (j, succ[i]);
}
} |
L'ordre décroissant sur la deuxième boucle n'est qu'une légère
subtilité pour présenter les listes de successeurs triées dans l'ordre
croissant. Mais il n'y a aucune obligation à faire de la sorte.
Réciproquement le constructeur suivant dans la classe GrapheMat
permet de passer de la représentation par listes de successeurs à la
représentation matricielle.
GrapheMat (Graphe g) {
int n = g.succ.length;
m = new boolean[n][n];
for (int x = 0; x < n; ++x) {
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
m[x][y] = true;
}
}
} |
| 1.5 |
Graphes et arborescences |
|
Définition 6
Une arborescence (X,A,r) de racine r est un graphe (X,A) où r
est un élément de X tel que pour tout sommet x il existe un
unique chemin d'origine r et d'extrémité x. Soit,
" x $ ! y0, y1 ,... ,yp
tels que:
y0=r, yp=x, " i, 0£ i < p
(yi,yi+1 ) Î A
L'entier p est appelé la profondeur du sommet x dans
l'arborescence. On montre facilement que, dans une arborescence, la
racine r n'admet pas de prédécesseur et que tout sommet y,
différent de r, admet un seul prédécesseur. Ceci
implique:
|A|=|X|-1
La différence entre une arborescence et un arbre est
mineure. Dans un arbre, les fils d'un sommet sont ordonnés (on
distingue le fils gauche du fils droit). Tel n'est pas le cas dans une
arborescence. Les arborescences servent depuis longtemps pour
représenter des arbres généalogiques. Le vocabulaire utilisé pour les
arborescences emprunte beaucoup de termes relevant des relations
familiales.
L'unique prédécesseur d'un sommet (différent de r) est appelé son
père, l'ensemble y0,y1 ,... yp (p ³ 0),
formant le chemin de r=y0 à x = yp, est appelé l'ensemble des ancêtres de x, les successeurs de x sont aussi appelés ses fils. L'ensemble des sommets extrémités d'un chemin d'origine x est
l'ensemble des descendants de x; il constitue une
arborescence de racine x, celle-ci est l'union de { x } et des
arborescences formées des descendants des fils de x. Pour des
raisons de commodité d'écriture qui apparaîtront dans la suite, nous
adoptons la convention que tout sommet x est à la fois ancêtre et
descendant de lui-même.
Nous représenterons une arborescence par le vecteur pere, qui à
chaque sommet différent de la racine associe son père. Par convention,
la racine sera le père d'elle-même.
Figure 1.6 : Une arborescence et son vecteur pere
La transformation d'un arborescence vue comme un graphe avec ses
listes de successeurs en une arborescence représenté par le vecteur
pere s'exprime simplement par le constructeur suivant:
class Arborescence {
int[ ] pere;
Arborescence (int n) { pere = new int[n]; }
Arborescence (Graphe g, int r) {
int n = g.succ.length;
pere = new int[n];
pere[r] = r;
for (int x = 0; x < n; ++x)
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
pere[y] = x;
}
}
} |
Dans la suite, on suppose que l'ensemble des sommets X est l'ensemble
des entiers compris entre 0 et n-1, une arborescence est dite préfixe si, pour tout sommet i, l'ensemble des descendants de i
est un intervalle de l'ensemble des entiers dont le plus petit
élément est i.
Figure 1.7 : Une arborescence préfixe
Figure 1.8 : Emboitement des descendants dans une arborescence préfixe
Dans une arborescence préfixe, les intervalles de descendants
s'emboîtent les uns dans les autres comme des systèmes de
parenthèses; ainsi, si y n'est pas un descendant de x, ni x un
descendant de y, les descendants de x et de y forment des
intervalles disjoints. En revanche, si x est un ancêtre de y,
l'intervalle des descendants de y est inclus dans celui des
descendants de x.
Proposition 7
Pour toute arborescence (X,A,r), il existe une re-numérotation des
éléments de X qui la rend préfixe.
Démonstration Pour trouver cette numérotation, on applique
l'algorithme récursif suivant:
-
La racine est numérotée 0.
- Un de ses fils x1 de la racine est numéroté 1.
- L'arborescence des descendants de x1 est numérotée par
appels récursifs de l'algorithme, on obtient ainsi des sommets
numérotés de 1 à p1.
- Un autre fils de la racine est numéroté p1+1; les
descendants de ce fils sont numérotés récursivement de p1+1
à p2.
- On procède de même et successivement pour tous les autres
fils de la racine.
La démonstration que la numérotation obtenue est bien préfixe se fait
par récurrence sur le nombre de sommets de l'arborescence.
La re-numérotation préfixe d'une arborescence ne fait rien de plus que
le parcours d'un arbre en ordre préfixe. On en déduit la construction
d'une arborescence préfixe à partir de la représentation d'une
arborescence vue comme un graphe avec ses listes de successeurs, comme
suit:
int i = -1;
static int[ ] numPrefixe (Graphe g, int r) {
int n = g.succ.length;
int[ ] num = new int[n];
numPrefixe1 (g, r, num);
return num;
}
static void numPrefixe1 (Graphe g, int x, int[ ] num, int i) {
numero[x] = ++i;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
numPrefixe1 (g, y, num);
}
}
static void appliquerNum (int[ ] pere, int[ ] num) {
int n = pere.length;
for (int i = 0; i < n; ++i)
pere[num[i]] = num[pere[i]];
}
static Arborescence arboPrefixe (Graphe g, int r) {
Arborescence a = new Arborescence (g, r);
appliquerNum (a.pere, numPrefixe(g, r));
return a;
} |
Exercice 1
Ecrire la fonction numPrefixe sans utiliser la variable globale
i, c'est-à-dire en transformant numOrdre en variable locale.
Exercice 2
Construire directement l'arborescence préfixe sans utiliser le
constructeur Arborescence.
| 1.6 |
Arborescences de Trémaux |
|
Si les arbres peuvent être considérés comme un cas particulier des
graphes, on associe souvent des arborescences ou arbres de
recouvrement (spanning trees en anglais) à des parcours de
graphes quelconques. En effet, pour parcourir tous les sommets d'un
graphe, à la différence des arbres il faut éviter de boucler,
notamment dans le cas des graphes cycliques.
En fait, le parcours de graphe le plus populaire a été mis au point
par un ingénieur du 19ème siècle, Trémaux, dont les travaux sont cités
dans un des premiers livres sur les graphes dû à Sainte Lagüe. Son
but était de résoudre le problème de la sortie d'un labyrinthe.
Depuis l'avènement de l'informatique, nombreux sont ceux qui ont
redécouvert l'algorithme de Trémaux. Certains en ont donné une
version bien plus précise et ont montré qu'il pouvait servir à
résoudre de façon très astucieuse beaucoup de problèmes algorithmiques
sur les graphes. Il est maintenant connu sous l'appellation de depth-first search (parcours en profondeur), nom que lui a donné un
de ses brillants promoteurs: R. E. Tarjan. Ce dernier a découvert,
entre autres, le très efficace algorithme de recherche des composantes
fortement connexes que nous décrirons à la fin de ce chapitre.
L'algorithme consiste à démarrer d'un sommet et à avancer dans le
graphe en ne repassant pas deux fois par le même sommet. Lorsque l'on
est bloqué, on revient sur ses pas jusqu'à pouvoir repartir vers un
sommet non visité. Cette opération de retour sur ses pas est très
élégamment prise en charge par l'écriture d'une fonction
récursive. Trémaux qui n'avait pas cette possibilité à l'époque
utilisait un fil d'Ariane lui permettant de se souvenir par où il
était arrivé à cet endroit dans le labyrinthe. Le programme récursif
suivant construit une arborescence (dite de Trémaux) pour un graphe
g quelconque à partir d'un de ses sommets x:
Figure 1.9 : Exécution de l'algorithme de Trémaux
static Arborescence arboTremaux (Graphe g, int x) {
int n = g.succ.length;
Arborescence a = new Arborescence (n);
for (int i = 0; i < n; ++i) a.pere[i] = -1;
a.pere[x] = x;
tremaux(g, x, a);
return a;
}
static void tremaux (Graphe g, int x, Arborescence a) {
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (a.pere[y] == -1) {
a.pere[y] = x;
tremaux(g, y, a);
}
}
} |
Le calcul effectif de l'arborescence de Trémaux de racine x
s'effectue en initialisant à la valeur -1 pour signaler que le
sommet correspondant n'a pas encore été visité. La figure
1.9 explique l'exécution de l'algorithme sur un exemple,
les appels de la fonction sont dans l'ordre:
tremaux (g, 0, a)
tremaux (g, 1, a)
tremaux (g, 2, a)
tremaux (g, 5, a)
tremaux (g, 4, a)
tremaux (g, 3, a) |
Une version non récursive de cet algorithme est obtenue en suivant le
principe général qui associe à tout programme récursif un programme
itératif manipulant une pile avec les primitives associées: Pile.ajouter, Pile.supprimer, Pile.estVide pour ajouter
un élément au sommet de la pile, pour retirer le sommet de la pile
tout en le renvoyant comme résultat, pour tester si la pile est vide.
static Arborescence arboTremauxPile (Graphe g, int x) {
int n = g.succ.length;
Arborescence a = new Arborescence (n);
for (int i = 0; i < n; ++i) a.pere[i] = -1;
Pile p = new Pile(n);
a.pere[x] = x;
Pile.ajouter (p, x);
while ( !Pile.estVide(p) ) {
x = Pile.supprimer (p);
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (a.pere[y] == -1) {
a.pere[y] = x;
Pile.ajouter (p, y);
}
}
}
return a;
} |
Le parcours n'est pas tout à fait le même que dans le programme récursif,
puisque l'ordre de parcours des successeurs d'un même sommet se fait
dans l'ordre de la liste des successeurs dans la version récursive,
alors qu'il se fait dans l'ordre inverse dans la version
itérative. Mais les deux parcours correspondent bien à des
arborescences de Trémaux, puisqu'ils s'effectuent bien en privilégiant
la profondeur.
L'ensemble des sommets atteignables à partir du sommet x est formé
des sommets tels que pere[y] est différent de -1 à la fin de
l'algorithme. On a donc un algorithme qui répond à la question existeChemin(g, x, y) examinée plus haut avec un nombre d'opérations
qui est de l'ordre du nombre d'arcs du graphe (lequel est inférieur à
n2), ce qui est bien meilleur qu'avec l'algorithme utilisant des
matrices d'adjacence.
L'ensemble des arcs du graphe G=(X,A) qui ne sont pas dans
l'arborescence de Trémaux (Y,T, x) est divisé en
quatre sous-ensembles:
-
les arcs dont l'origine n'est pas dans Y, ce sont les arcs
issus d'un sommet qui n'est pas atteignable à partir de x;
- les arcs de descente, il s'agit des arcs de la forme
(y,z) où z est un descendant de y dans (Y,T,x), mais n'est
pas un de ses successeurs dans cette arborescence;
- les arcs de retour, il s'agit des arcs de la forme
(y,z) où z est un ancêtre de y dans (Y,T,x);
- les arcs transverses, il s'agit des arcs de la forme
(y,z) où z n'est pas un ancêtre, ni un descendant de y dans
(Y,T,x).
On remarquera que, si (y,z) est un arc transverse, on aura rencontré
z avant y dans l'algorithme de Trémaux.
Figure 1.10 : Les arcs obtenus par Trémaux
Sur le graphe de la figure 1.10, les différentes sortes
d'arcs y sont représentés par des lignes particulières. Les arcs de
l'arborescence sont en traits gras; les arcs dont l'origine n'est pas
dans Y sont dessinés en trait simple; les arcs de descente, de
retour ou transverses sont en tiretés et munis d'une étiquette
permettant de les reconnaître, D, R ou
Tr. Les sommets ont été numérotés suivant l'ordre dans
lequel on les rencontre par l'algorithme de Trémaux. Ainsi, les arcs de
l'arborescence et les arcs de descente vont d'un sommet à un sommet
d'étiquette plus élevée et c'est l'inverse pour les arcs de retour ou
transverses.
| 1.7 |
Arborescences des plus courts chemins. |
|
Une autre arborescence souvent associée à un graphe quelconque est
l'arborescence des plus courts chemins. Elle correspond à un parcours
en largeur (breadth-first search en anglais). On parcourt le
graphe à partir d'un sommet en émettant une onde à partir de ce sommet
et en rencontrant en priorité les sommets à égales distances de ce
sommet.
Définition 8
Dans un graphe G=(X,A), pour chaque sommet x, une arborescence des
plus courts chemins de racine x est une arborescence (Y,B,x) telle
que:
- Un sommet y appartient à Y si et seulement s'il existe un
chemin d'origine x et d'extrémité y.
- La longueur du plus court chemin de x à y dans G est
égale à la profondeur de y dans l'arborescence (Y,B,x).
Figure 1.11 : Une arborescence des plus courts chemins de racine 10
Cette arborescence existe bien puisque, si a1,a2,..., ap est
un plus court chemin entre org(a1) et ext(ap), alors le chemin
a1,a2,..., ai est aussi un plus court chemin entre org(a1)
et ext(ai) pour tout i vérifiant 1£ i £ p.
Théorème 9 Pour tout graphe G=(X,A) et tout sommet x de G, il
existe une arborescence des plus courts chemins de racine x.
Démonstration On considère la suite d'ensembles de sommets construite
de la façon suivante:
- Y0 = { x } .
- Y1 est l'ensemble des successeurs de x, duquel il faut
éliminer x si le graphe possède un arc ayant x pour origine et
pour extrémité.
- Yi+1 est l'ensemble des successeurs d'éléments de Yi
qui n'appartiennent pas à Èk=1,i Yi.
D'autre part pour chaque Yi (i >0), on construit l'ensemble
d'arcs Bi contenant pour chaque y Î Yi un arc ayant comme
extrémité y et dont l'origine est dans Yi-1. On pose ensuite:
Y = ÈYi, B = ÈBi. Le graphe (Y ,B) est par
construction une arborescence. C'est une arborescence des plus courts
chemins grâce à la remarque ci-dessus.
La figure 1.11 donne un exemple de graphe
et une arborescence des plus courts chemins de racine 10, celle-ci
est représentée en traits gras, les ensembles Yi et Bi sont
les suivants:
| Y0 = { 10 } |
|
| Y1 = { 7,11 } |
B1 = { (10,7), (10,11) } |
| Y2 = { 3,9,8 } |
B2 = { (7,3), (7,9), (11,8) } |
| Y3 = { 5,6 } |
B3 = { (3,5), (8,6) } |
A nouveau, la preuve de ce théorème se transforme très simplement en
un algorithme de construction de l'arborescence (Y,B).
Cet algorithme est souvent appelé algorithme de parcours en
largeur. Nous le décrivons ci dessous, il utilise une file d'attente
avec les primitives associées: FIFO.ajouter, FIFO.supprimer, FIFO.estVide pour ajouter un élément en bout de
file, pour retirer le premier élément dans la file tout en le
renvoyant comme résultat, pour tester si la file est vide. La file
gère les ensembles Yi. On ajoute les éléments des Yi
successivement dans la file, qui contient donc les Yi les uns à la
suite des autres. La vérification de ce qu'un sommet n'appartient pas
à Èk=1,i Yi se fait en testant si pere[y] ne vaut pas
-1.
static Arborescence arboPlusCourt (Graphe g, int x) {
int n = g.succ.length;
Arborescence a = new Arborescence (n);
for (int i = 0; i < n; ++i) a.pere[i] = -1;
FIFO f = new FIFO(n);
a.pere[x] = x;
FIFO.ajouter (f, x);
while ( !FIFO.estVide(f) ) {
x = FIFO.supprimer (f);
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (a.pere[y] == -1) {
a.pere[y] = x;
FIFO.ajouter (f, y);
}
}
}
return a;
} |
On remarque que ce programme est le même que le programme itératif
pour calculer une arborescence de Trémaux, en remplaçant une pile par
une file d'attente.
Nous avons considéré les parcours de graphes en profondeur et en
largeur, pour traverser un graphe sans boucler, ni passer plus d'une
fois par chaque sommet. A nouveau, comme la structure d'arbre (ou
d'arborescence) est un cas particulier de la structure de graphe, on
peut se demander quels sont, sur les graphes, les équivalents des
parcours préfixes ou postfixes sur les arbres.
Au lieu de renvoyer une arborescence, nous considérons une nouvelle
version du programme tremaux qui retourne une numérotation des
sommets qui donne le numéro d'ordre de chaque sommet dans l'ordre où
on l'a rencontré. Pour cela, on colorie les sommets traditionnellement
avec trois couleurs: blanc pour les sommets non encore explorés, gris
pour un sommet partiellement traité, noir pour un sommet complètement
traité.
final static int BLANC = 0, GRIS = 1, NOIR = 2;
int numOrdre = -1;
static int[ ] tremauxPrefixe (Graphe g) {
int n = g.succ.length;
int[ ] couleur = new int[n], num = new int[n];
for (int x = 0; x < n; ++x) couleur[x] = BLANC;
for (int x = 0; x < n; ++x)
if (couleur[x] == BLANC)
tremauxPref (g, x, couleur, num);
return num;
}
static void tremauxPref (Graphe g, int x, int[ ] couleur, int[ ] num) {
couleur[x] = GRIS;
num[x] = ++numOrdre;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (couleur[y] == BLANC)
tremauxPref (g, y, couleur, num);
}
couleur[x] = NOIR;
} |
Remarquons que, si la coloration en gris se faisait avant l'appel à
tremauxPref, cela ne ferait aucune différence, puisque le
parcours en profondeur traite immédiatement tout nouveau sommet
rencontré.
On obtient une numérotation postfixe pour un parcours en
profondeur en changeant simplement l'emplacement où se fait
l'affectation du numéro de chaque sommet.
static int[ ] tremauxPostfixe (Graphe g) {
int n = g.succ.length;
int[ ] couleur = new int[n], num = new int[n];
for (int x = 0; x < n; ++x) couleur[x] = BLANC;
for (int x = 0; x < n; ++x)
if (couleur[x] == BLANC)
tremauxPost (g, x, couleur, num);
return num;
}
static void tremauxPost (Graphe g, int x, int[ ] couleur, int[ ] num) {
couleur[x] = GRIS;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (couleur[y] == BLANC)
tremauxPost (g, y, couleur, num);
}
num[x] = ++numOrdre;
couleur[x] = NOIR;
} |
Un certain nombre de propriétés sur la couleur des sommets pendant le
parcours récursif peuvent être énoncées. Par exemple, dans une
arborescence de Trémaux, un sommet noir ne peut jamais être l'origine
d'un arc vers un sommet blanc. De la même manière, un sommet blanc
extrémité d'un chemin complètement blanc issu d'un sommet gris se
retrouvera descendant de ce sommet gris dans l'arbre de recouvrement;
etc.
Exercice 3 Ecrire les fonctions tremauxPrefixe et tremauxPostfixe en transformant la variable globale numOrdre en
variable locale.
Le parcours en largeur est aussi plus compréhensible en ne raisonnant
que sur la couleur des sommets:
static int[ ] largeurPref (Graphe g, int x) {
int n = g.succ.length, numOrdre = -1;
int[ ] couleur = new int[n], num = new int[n];
for (int x = 0; x < n; ++x) couleur[x] = BLANC;
FIFO f = new FIFO(n);
couleur[x] = GRIS;
FIFO.ajouter (f, x);
while ( !FIFO.estVide(f) ) {
x = FIFO.supprimer (f);
num[x] = ++numOrdre;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (couleur[y] == BLANC) {
couleur[y] = GRIS;
FIFO.ajouter (f, y);
}
}
couleur[x] = NOIR;
}
return num;
} |
Dans ce parcours en largeur, la coloration en gris d'un sommet doit se
faire avant de le placer dans la file d'attente, sous peine de l'y
mettre plusieurs fois, et de devoir faire intervenir la valeur du
résultat num qu'il est plus sage de distinguer du contrôle du
parcours.
Quant au parcours postfixe, il s'obtient en déplaçant l'instruction de
numérotation d'un sommet, et en la plaçant avant la coloration en
noir. Mais le résultat num serait alors le même que celui obtenu
dans le parcours préfixe, puisque, dans le parcours en largeur, rien
ne se passe entre le rangement dans la file des successeurs d'un
sommet et le traitement du sommet en question.
Tous les parcours en profondeur ou en largeur ne passent qu'une seule
fois par chaque sommet et font un nombre d'opérations proportionnel au
nombre d'arcs. La complexité de tels parcours dans un graphe G=(X,A)
est donc en O(|X| + |A|), qu'on écrit souvent simplement par O(X +
A).
Les graphes sans cycle (directed acyclic graphs en anglais ou
plus simplement dags) interviennent souvent dans les problèmes
d'ordonnancement: organisation des différents travaux sur un chantier,
dépendance entre modules dans un projet de programmation, etc. Un
arbre est un dag particulier; mais, dans un dag,
contrairement aux arbres, on peut partager des sous-dags. Un
graphe est dit acyclique s'il ne contient pas de circuit.
Un algorithme pour tester l'acyclicité d'un graphe se fait facilement
par un parcours en profondeur. En effet, si un graphe contient un
circuit, cela signifie que, dans un arbre de recouvrement, un sommet
x est l'origine d'un arc dont l'extrémité est un ancêtre de x dans
l'arbre de recouvrement, comme indiqué sur la figure
1.12 en considérant x=6 duquel part un arc vers
le sommet gris 12. Cela veut dire que dans le parcours en
profondeur le successeur d'un sommet gris pourra être gris. Si cela ne
se produit jamais, le graphe est acyclique. D'où le programme suivant:
Figure 1.12 : Un graphe avec cycle et son arbre de recouvrement
static boolean acyclique (Graphe g) {
int n = g.succ.length;
int[ ] couleur = new int[n];
for (int x = 0; x < n; ++x) couleur[x] = BLANC;
for (int x = 0; x < n; ++x)
if ( (couleur[x] == BLANC) && cycleEn (g, x, couleur) )
return false;
return true;
}
static boolean cycleEn (Graphe g, int x, int[ ] couleur) {
couleur[x] = GRIS;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if ( (couleur[y] == GRIS) ||
(couleur[y] == BLANC) && cycleEn (g, y, couleur) )
return true;
}
couleur[x] = NOIR;
return false;
} |
La complexité de cet algorithme est donc en O(X+A). On se
convainc qu'on ne peut faire mieux, puisqu'il faudra bien considérer
tous les arcs du graphe avant de décider de son acyclicité.
Un problème classique sur les graphes sans cycle est le tri
topologique. Il consiste à organiser l'agenda d'un certain nombre de
tâches données par un graphe de dépendances.
Prenons le cas de la lecture d'un livre, par exemple le livre de
Barendregt sur le lambda-calcul [27]. Dans ses premières
pages, on voit le diagramme (assez compliqué) de la
figure 1.13 décrivant l'ordre de lecture des
différents chapitres. Ainsi pour lire le chapitre 16, il faut avoir lu
les chapitres 4, 8 et 15. Un lecteur courageux veut lire le strict
minimum pour appréhender le chapitre 21. Il faut donc qu'il
transforme l'ordre partiel indiqué par les dépendances du diagramme en
un ordre total déterminant la liste des chapitres nécessaires au
chapitre 21. Bien sûr, ceci n'est pas possible si le graphe de
dépendance contient un cycle. L'opération qui consiste à mettre ainsi
en ordre les sommets d'un graphe dirigé sans cycle est appelée le tri
topologique.
Figure 1.13 : Un exemple de graphe acyclique
Le tri topologique ordonne les sommets d'un dag en une
suite dans laquelle l'origine de chaque arc apparaît avant son
extrémité. Pour un sommet s donné, on construit une liste formée de
tous les sommets origines d'un chemin d'extrémité s. Cette liste
doit en plus satisfaire la condition énoncée plus haut. On applique
l'algorithme de descente en profondeur d'abord (Trémaux) sur le graphe
inverse. (Au lieu de considérer les successeurs succ[x] du
sommet x, on considère ses prédécesseurs pred[x].) Au cours de
cette recherche, quand on a fini de visiter un sommet, on le met en
tête de liste. En fin de l'algorithme, on calcule l'image mirroir de
la liste. Pour tester l'existence de cycles, on doit vérifier
lorsqu'on rencontre un sommet déjà visité que celui-ci figure dans la
liste résultat.
final static BLANC = 0, GRIS = 1, NOIR = 2;
static Liste triTopologique (Graphe g, int u) {
int n = g.succ.length;
int[ ] etat = new int[n];
for (int x = 0; x < n; ++x) etat[x] = BLANC;
return Liste.mirroir (DFS (g, u, etat, null));
}
static Liste DFS (Graphe g, int x, int[ ] etat, Liste a_faire) {
etat[x] = GRIS;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (etat[y] == GRIS) throw new Error ("Le graphe a un cycle");
if (etat[y] == BLANC) {
etat[y] = GRIS;
a_faire = DFS (g, y, etat, a_faire);
} }
etat[x] = NOIR;
return Liste.ajouter (x, a_faire);
} |
La complexité de cet algorithme est celle d'une recherche en
profondeur d'abord, don en O(X+A), suivie de l'image mirroir qui
ne dépasse pas O(A). Au total la complexité est en O(X+A).
| 1.10 |
Connexité dans un graphe non-orienté |
|
Comme déjà mentionné, nous représentons les graphes non-orientés par
des graphes orientés symétriques. Pour tous sommets x et y, s'il
existe un arc (x,y), il existe aussi un arc (y,x). Donc,
s'il existe un chemin de x à y, il existe aussi un chemin de y à
x.
Définition 10
Soit G=(X,A) un graphe non-orienté. La composante connexe du sommet
x est l'ensemble des sommets y reliés par un chemin à x. Un
graphe est connexe s'il ne contient qu'une seule composante connexe.
L'appartenance à une même composante connexe est une
relation d'équivalence. Les composantes connexes forment une
partition du graphe en sous-graphes déconnectés.
Dans un graphe non-orienté, un arbre de recouvrement ne contient
jamais d'arc transverse. Plus exactement, l'ensemble des arcs du
graphe qui ne sont pas dans un arbre de recouvrement de racine x est
divisé en trois sous-ensembles:
-
Les arcs déconnectés, dont ni l'origine, ni l'extrémité ne
sont dans l'arbre de recouvrement. Il n'existe pas de chemin de x
vers l'origine ou l'extrémité de ces arcs.
- Les arcs de descente, il s'agit des arcs de la forme
(y,z) où z est un descendant non direct de y dans l'arbre de
recouvrement.
- Les arcs de retour, il s'agit des arcs de la forme
(y,z) où z est un ancêtre de y dans l'arbre de recouvrement.
On en déduit que l'ensemble des sommets d'un arbre de recouvrement
constitue exactement la composante connexe de sa racine. D'où le
programme suivant pour imprimer les composantes connexes d'un graphe
non-orienté G.
static void imprimerCompConnexes (Graphe g) {
int n = g.succ.length;
int[ ] couleur = new int[n];
for (int x = 0; x < n; ++x) couleur[x] = BLANC;
for (int x = 0; x < n; ++x) {
if (couleur[y] == BLANC) {
imprimerComp (g, x, couleur);
System.out.println();
}
}
}
static void imprimerComp (Graphe g, int x, int[ ] couleur) {
couleur[x] = GRIS;
System.out.print (x + " ");
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (couleur[y] == BLANC)
imprimerComp (g, y, couleur);
}
} |
Il s'agit encore d'un parcours en profondeur. Le programme imprime les
composantes connexes, ligne par ligne, en temps O(X+A). De manière
identique, on peut écrire un programme de sortie d'un labyrinthe,
puisqu'il suffit de tester si la sortie s est dans la composante
connexe de l'entrée x. Nous voulons alors retourner un chemin de x
vers s, chemin que nous représentons par la liste des sommets par
lesquels il passe.
static Liste sortieDeLabyrinthe (Graphe g, int x, int s) {
int n = g.succ.length;
int[ ] couleur = new int[n];
for (int x = 0; x < n; ++x) couleur[x] = BLANC;
return chemin (g, x, s, couleur);
}
static void chemin (Graphe g, int x, int s, int[ ] couleur) {
couleur[x] = GRIS;
if (x == s)
return new Liste (s, null);
else {
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (couleur[y] == BLANC)
Liste ch = chemin (g, y, s, couleur);
if (ch != null)
return new Liste (x, ch);
}
}
return null;
} |
Exercice 4 Ecrire un programme qui imprime tous les chemins simples
(c'est à dire ne passant pas deux fois par un même sommet) de l'entrée
vers la sortie d'un labyrinthe.
Exercice 5 Ecrire un programme qui calcule un chemin le plus court
reliant l'entrée à la sortie du labyrinthe.
| 1.11 |
Biconnexité dans un graphe non-orienté |
|
Dans une composante connexe, il existe toujours un chemin pour relier
deux sommets. Dans une composante biconnexe, il doit en exister
toujours deux. Ce problème se pose par exemple quand on conçoit un
plan de circulation; on veut éviter les endroits névralgiques,
obligatoires pour se rendre d'un endroit à un autre. De la même
manière, dans un réseau informatique, on évite les sites qui
déconnectent le réseau quand ils tombent en panne.
Définition 11
Soit G=(X,A) un graphe non-orienté. Un sommet x est un point
d'articulation si la suppression de x déconnecte deux sommets de
G.
Figure 1.14 : Points d'articulation dans un graphe non-orienté
Dans le graphe de la figure 1.14 (à
gauche), les points d'articulation sont indiqués en grisé. La
suppression du sommet 3 déconnecte le sommet 9; de même pour le
sommet 2 qui déconnecte l'ensemble {10, 5}; et pour 10 qui
déconnecte 5. Tarjan a trouvé une solution remarquable pour
calculer les points d'articulation dans un graphe. Sa solution ne fait
intervenir qu'un parcours en profondeur et la numérotation préfixe
correspondante. En effet, caractérisons les points d'articulations sur
un arbre de recouvrement. Dans l'arbre de recouvrement, un point
d'articulation est un sommet x possédant un fils dont tous les
descendants ne sont pas des origines d'arcs de retour vers des
ancêtres stricts de x dans l'arbre. Par exemple, sur l'arbre de
recouvrement de la figure 1.14 (à
droite), le sommet 3 est un point d'articulation, puisque son fils
9 ne possède qu'un arc de retour vers 3 dans l'arbre de
recouvrement. Mais, le sommet 12 n'est pas un point d'articulation,
puisque son unique fils 3 a comme descendant 6 dont 2 est un
successeur. Or 2 est un ancêtre strict de 12 dans l'arbre de
recouvrement. Intuitivement, on voit bien que, si on enlève le sommet
3, on déconnecte le sous-arbre 9, alors qu'on ne déconnecte rien
si on enlève le sommet 12.
Avec ce seul critère, la racine d'un arbre de recouvrement serait
toujours un point d'articulation. Il faut donc faire un cas
particulier pour décider si la racine est un point d'articulation. Le
critère est alors simple: la racine est un point d'articulation si
elle contient plusieurs fils dans l'arbre de recouvrement. Sur la
figure 1.14, c'est bien le cas puisque
4 et 10 sont deux fils de 2.
Définition 12
Soit G=(X,A) un graphe, x un sommet et (Y,T,x) une arborescence
de Trémaux induisant une numérotation préfixe num des sommets.
Le point d'attache
at(y) d'un sommet y de Y est le
sommet de plus petit numéro, extrémité d'un chemin de G d'origine
y et contenant au plus un arc (u,v) tel que num[u] >
num[v].
Cela signifie qu'un point d'attache est un sommet atteignable par un
chemin ne comportant au plus qu'un arc transverse ou de retour,
puisque dans le cas des graphes non-orientés, les arcs transverses
n'existent pas. Sur la figure 1.14,
pour chaque sommet y, son numéro num[y] dans l'ordre préfixe
est placé au-dessus de y, le numéro de son point d'attache
num[at(y)] est placé à droite. Les points d'attache se
calculent (dans un graphe orienté ou pas) grâce à la remarque
suivante:
Proposition 13
Le point d'attache at(y) du sommet y est le sommet de plus petit
numéro parmi les sommets suivants:
-
le sommet y.
- les points d'attaches des fils de y dans (Y,T,x).
- les extrémités des arcs transverses ou de retour dont
l'origine est y.
Pour détecter les points d'articulation, il reste donc à réaliser les
deux types de tests pour un sommet ordinaire de l'arbre et pour la
racine. Un peu d'arithmétique sur la numérotation préfixe effectue le
premier test. Un sommet x, différent de la racine, sera un point
d'articulation si et seulement s'il possède un fils y tel que:
num[x] £ num[at(y)]
On en déduit l'algorithme suivant pour détecter les points
d'articulation. Le résultat est rangé dans un tableau de booléens articulation indiquant, pour chaque sommet x, s'il est un point
d'articulation.
static int numOrdre; static int[ ] num;
static boolean[ ] trouverArticulations (Graphe g) {
int n = g.succ.length;
id = -1; num = new int[n];
boolean[ ] articulation = new boolean[n];
for (int x = 0; x < n; ++x) num[x] = -1;
for (int x = 0; x < n; ++x)
if (num[x] == -1) {
int r = attache1(g, x, articulation);
}
return articulation;
}
static int attache (Graphe g, int x, boolean[ ] articulation) {
int min = num[x] = ++numOrdre;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val; int m;
if (num[y] == -1) {
m = attache (g, y, articulation);
if (m >= num[x])
articulation[x] = true;
} else
m = num[y];
min = Math.min (min, m);
}
return min;
} |
La fonction attache1 est pratiquement identique à attache
sauf que, pour la racine, il faut compter le nombre de ses fils dans
l'arbre de recouvrement.
static int attache1 (Graphe g, int x, boolean[ ] articulation) {
int min = num[x] = ++numOrdre;
int nfils = 0;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val; int m;
if (num[y] == -1) {
++nfils;
m = attache (g, y, articulation);
if (m >= num[x])
articulation[x] = true;
} else m = num[y];
min = Math.min (min, m);
}
articulation[x] = nfils > 1;
return min;
} |
On peut déplier l'appel de attache1 dans trouverArticulations:
static boolean[ ] trouverArticulations (Graphe g) {
int n = g.succ.length;
id = -1; num = new int[n];
boolean[ ] articulation = new boolean[n];
for (int x = 0; x < n; ++x) num[x] = -1;
for (int x = 0; x < n; ++x)
if (num[x] == -1) {
num[x] = ++numOrdre;
int nfils = 0;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val;
if (num[y] == -1) {
++nfils;
int m = attache (g, y, articulation);
}
}
articulation[x] = nfils > 1;
}
return articulation;
} |
La détection des points d'articulation se fait donc avec un simple
parcours en profondeur. Sa complexité est donc en en O(X+A). Il
reste à calculer les composantes bi-connexes, ce qui est un petit peu
plus délicat, mais réalisable avec la même complexité.
Exercice 6
Donner une défintion précise de la notion de composantes biconnexes,
et trouver un algorithme pour les calculer.
| 1.12 |
Composantes fortement connexes |
|
Dans un graphe orienté, la notion de connexité n'est pas aussi simple
que dans un graphe non-orienté, puisque deux sommets x et y
peuvent être connectés par un chemin de x à y, sans qu'il existe
un chemin de y à x.
Définition 14
Soit G=(X,A) un graphe. Notons ºG la relation
d'équivalence suivante entre sommets: x ºG y si x=y ou s'il
existe un chemin joignant x à y et un chemin joignant y à x.
Les classes d'équivalences définies par ºG sont les composantes fortement connexes de G.
La relation ºG est clairement une relation d'équivalence. La
symétrie et la réflexivité sont évidentes. La transitivité résulte de
ce que l'on peut concaténer un chemin entre x et y et un chemin
entre y et z pour obtenir un chemin entre x et z. Sur la
figure 1.15, le graphe comporte 5 composantes
fortement connexes, trois ne contiennent qu'un seul sommet, une est
constituée d'un triangle et la dernière comporte 9 sommets.
Lorsque la relation ºG n'a qu'une seule classe, le graphe
est dit fortement connexe. Un exemple de graphe fortement
connexe est celui des voies de circulation d'une ville en tenant
compte des sens uniques.
Figure 1.15 : Composantes fortement connexes du graphe de la figure
1.10
Un algorithme de recherche des composantes fortement connexes débute
nécessairement par un parcours à partir d'un sommet x, les
sommets qui n'appartiennent pas à l'arborescence ainsi construite ne
sont certainement pas dans la composante fortement connexe de x, mais
la réciproque n'est pas vraie: un sommet y qui est dans
l'arborescence issue de x n'est pas nécessairement dans sa
composante fortement connexe car il se peut qu'il n'y ait pas de
chemin allant de y à x.
Une manière simple de procéder pour le calcul de ces composantes
consiste à itérer l'algorithme suivant pour chaque sommet x dont
la composante n'a pas encore été construite:
-
Déterminer les sommets extrémités de chemins d'origine x,
par exemple en utilisant l'algorithme de Trémaux à partir de x.
- Retenir parmi ceux ci les sommets qui sont l'origine d'un chemin
d'extrémité x. On peut, pour ce faire, construire le graphe
opposé de G obtenu en renversant le sens de tous les arcs de G
et appliquer l'algorithme de Trémaux sur ce graphe à partir de
x.
Cette manière de procéder est peu efficace lorsque le graphe possède
de nombreuses composantes fortement connexes, car on peut être amené à
parcourir tout le graphe autant de fois qu'il y a de composantes.
Nous allons voir que la construction de l'arborescence de Trémaux
issue de x va permettre de calculer toutes les composantes connexes
des sommets descendants de x en un nombre d'opérations proportionnel
au nombre d'arcs du graphe.
Les liens entre arborescence de Trémaux (Y,T,x) et les composantes
fortement connexes sont dus à la proposition suivante.
Figure 1.16 : Un exemple de sous-arborescence
Définition 15
Une sous-arborescence (Y',T',r') de l'arborescence (Y,T,r)
est une arborescence telle que Y' Ì Y et T' Ì T.
Ainsi tout élément de Y' est extrémité d'un chemin d'origine
r' et ne contenant que des arcs de T'.
Proposition 16
Soit G=(X,A) un graphe. Soient x Î X, et (Y,T,x) une
arborescence de Trémaux. Pour tout sommet u de Y, la composante
fortement connexe contenant u est une sous-arborescence de
(Y,T,x).
Démonstration Notons C(u) la composante fortement connexe C(u) de
u (contenant u). Cette proposition contient en fait deux
conclusions; d'une part elle assure l'existence d'un sommet u0 dans
C(u) tel que tous les éléments de C(u) sont des descendants de
u0 dans (Y,T,x), d'autre part elle affirme que pour tout v de
C(u) tous les sommets du chemin de (Y,T,x) joignant u0 à v sont
dans C(u).
La deuxième affirmation est simple à obtenir car, dans un graphe, tout
sommet situé sur un chemin joignant deux sommets appartenant à la même
composante fortement connexe est aussi dans cette composante. Pour
prouver la première assertion, prenons pour u0 le sommet de plus
petit numéro de C(u), et montrons que tout sommet v de C(u) est
un descendant de u0 dans (Y,T,x). Supposons le contraire. Comme
v est dans la même composante que u0, il existe un chemin f
d'origine u0 et d'extrémité v. Soit w le premier sommet de f
qui n'est pas un descendant de u0 dans (Y,T,x) et soit w' le
sommet qui précède w dans f. L'arc (w',w) n'est pas un arc de
T, ni un arc de descente, c'est donc un arc de retour ou un arc
transverse et on a
num[u0] £ num[w] £ num[w']
L'arborescence (Y,T) étant préfixe on en déduit que w est
descendant de u0 d'où la contradiction cherchée.
On remarquera qu'un chemin qui conduit d'un sommet y à son point
d'attache est ou bien vide (le point d'attache est alors y lui
même), ou bien contient une suite d'arcs de T suivis par un arc
de retour ou un arc transverse. En effet, une succession d'arcs de T
partant de y conduit à un sommet de numéro plus grand que y,
d'autre part les arcs de descente ne sont pas utiles dans la recherche
du point d'attache, ils peuvent être remplacés par des chemins
formés d'arcs de T.
Figure 1.17 : Les points d'attaches des sommets d'un graphe
Dans la figure 1.17, on a calculé les points d'attaches
des sommets d'un graphe, ceux-ci ont été numérotés dans l'ordre où on
les rencontre dans l'algorithme de Trémaux (on suppose pour simplifier
que x = num[x] pour tout x); le point d'attache est indiqué
en petit caractère à droite du sommet en question.
Comme dans le cas de la biconnexité, le calcul des composantes
fortement connexes à l'aide des at(u) se fait par un peu
d'arithmétique sur la numérotation préfixe et les points
d'attache. C'est une conséquence du théorème suivant:
Théorème 17 Si u est un sommet de Y satisfaisant:
- (i) u = at(u)
- (ii) Pour tout descendant v de u dans (Y,T,x) on a
at(v) < v
Alors, l'ensemble desc(u) des descendants de u dans (Y,T,x) forme
une composante fortement connexe de G.
Démonstration Montrons d'abord que tout sommet de desc(u) appartient
à C(u). Soit v un sommet de desc(u), il est extrémité
d'un chemin d'origine u, prouvons que u est aussi extrémité
d'un chemin d'origine v. Si tel n'est pas le cas, on peut supposer
que v est le plus petit sommet de desc(u) à partir duquel on ne
peut atteindre u, soit f le chemin joignant v à at(v), le
chemin obtenu en concaténant f à un chemin de (Y,T,x) d'origine
u et d'extrémité v contient au plus un arc de retour ou
transverse ainsi:
u=at(u) £ at(v) < v
Comme (Y,T,x) est préfixe, at(v) appartient à
desc(u) et d'après l'hypothèse de minimalité il existe un
chemin d'origine at(v) et d'extrémité u qui concaténé à
f fournit la contradiction cherchée.
Il reste à montrer que
tout sommet w de C(u) appartient aussi à desc(u). Un tel sommet est
extrémité d'un chemin g d'origine u, nous allons voir que tout
arc dont l'origine est dans desc(u) a aussi son extrémité dans
desc(u), ainsi tous les sommets de g sont dans desc(u) et en
particulier w. Soit (v1,v2) Î A un arc tel que v1 Î
desc(u), si v2 > v1, v2 est un descendant de v1 il
appartient donc à desc(v); si v2 < v1 alors le chemin menant
de u à v2 en passant par v1 contient exactement un arc de
retour ou transverse, ainsi :
u=at(u) £ v2 < v1
et la préfixité de (Y,T,x) implique v2 Î desc(u).
Remarquons qu'il existe toujours un sommet satisfaisant les conditions
du théorème. En effet, si x est la racine de (Y,T,x), on a
at(x)=x. Si x satisfait (ii), l'ensemble Y en
entier constitue une composante fortement connexe. Sinon il existe un
descendant y de x tel que y=at(y). En répétant cet
argument plusieurs fois et puisque le graphe est fini, on finit par
obtenir un sommet satisfaisant les deux conditions.
La recherche des composantes fortement connexes est alors effectuée par
la détermination d'un sommet u tel que u= at(u), obtention d'une
composante égale à desc(u), suppression de tous les sommets de
desc(u) et itération des opérations précédentes jusqu'à
obtenir tout le graphe.
Sur la figure 1.17, on peut se rendre compte du procédé
de calcul. Il y a 4 composantes fortement connexes, les sommets u
satisfaisant u = at(u) sont au nombre de 3, il s'agit de 0,
1, 5. La première composante trouvée se compose du sommet 5
uniquement, il est supprimé et le sommet 6 devient alors tel que u
= at(u). Tous ses descendants forment une composante fortement
connexe {6,7,8}. Après leur suppression, le sommet 1 satisfait
u = at(u) et il n'a plus de descendant satisfaisant la même
relation. On trouve ainsi une nouvelle composante {1,2,3,4}. Une
fois celle-ci supprimée, 0 est le seul sommet qui satisfait la
relation u = at(u) d'où la composante
{0,9,10,11,12,13,14,15,16}.
L'algorithme ci-dessous calcule en même temps at(u) pour tous
les descendants u de x et obtient successivement toutes les
composantes fortement connexes de desc(x). Il utilise le fait que
la suppression des descendants de u lorsque u=at(u) ne
modifie pas les calculs des at(v) en cours.
static int id = -1;
static void imprimerCompFConnexes (Graphe g) {
int n = g.succ.length;
int[ ] num = new int[n];
for (int x = 0; x < n; ++x) num[x] = -1;
for (int x = 0; x < n; ++x) {
if (num[y] == -1)
imprimerCompF (g, x, num);
}
}
static int imprimerCompF (Graphe g, int x, int[ ] num) {
num[x] = ++numOrdre; Pile.ajouter(x, p);
int min = id;
for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
int y = ls.val; int m;
if (num[y] == -1)
m = imprimerCompF (g, y, num);
else m = num[y];
min = Math.min (min, m);
}
if (min == num[x]) {
int y;
do {
y = Pile.supprimer(p);
System.out.print (y + " ");
num[y] = g.succ.length;
} while (y != x);
System.out.println();
}
return min;
} |
Ce bel algorithme, dû à Tarjan, illustre la puissance de la notion de
parcours en profondeur; il a une complexité en O(X+A).
let m =
[| [| 1.0; 0.0; 0.0 |];
[| 0.0; 1.0; 0.0 |];
[| 0.0; 0.0; 1.0 |] |];;
let g =
[| [| 0; 1; 1; 0; 0; 0 |];
[| 0; 0; 1; 1; 0; 1 |];
[| 0; 0; 0; 0; 0; 1 |];
[| 0; 0; 0; 0; 1; 0 |];
[| 0; 1; 0; 0; 0; 0 |];
[| 0; 0; 0; 1; 0; 0 |] |];;
let nb_lignes m = Array.length m
and nb_colonnes m =
if Array.length m = 0 then failwith "nb_colonnes"
else Array.length m.(0);;
(* Calcule le produit des matrices a et b *)
let multiplier a b =
if nb_colonnes a <> nb_lignes b
then failwith "multiplier" else
let c =
Array.make_matrix (nb_lignes a) (nb_colonnes b) 0 in
for i = 0 to nb_lignes a - 1 do
for j = 0 to nb_colonnes b - 1 do
let cij = ref 0 in
for k = 0 to nb_colonnes a - 1 do
cij := a.(i).(k) * b.(k).(j) + !cij;
done;
c.(i).(j) <- !cij
done
done;
c;; |
(* Calcule la somme des matrices a et b *)
let ajouter a b =
if nb_colonnes a <> nb_lignes b
then failwith "ajouter" else
let c =
Array.make_matrix (nb_lignes a) (nb_colonnes b) 0 in
for i = 0 to nb_lignes a - 1 do
for j = 0 to nb_colonnes b - 1 do
c.(i).(j) <- a.(i).(j) + b.(i).(j)
done
done;
c;; |
(* Élève la matrice m à la puissance i *)
let rec puissance m i =
match i with
| 0 -> failwith "puissance"
| 1 -> m
| n -> multiplier m (puissance m (i - 1));; |
let nombre_de_chemin_de_longueur n i j m =
(puissance m n).(i).(j);;
let sigma i m =
let rec pow i mp =
match i with
| 1 -> mp
| n -> ajouter mp (pow (i - 1) (multiplier m mp)) in
pow i m;;
let existe_chemin i j m =
(sigma (nb_colonnes m) m).(i).(j) <> 0;; |
let phi m x =
for u = 0 to nb_colonnes m - 1 do
if m.(u).(x) = 1 then
for v = 0 to nb_colonnes m - 1 do
if m.(x).(v) = 1 then m.(u).(v) <- 1
done
done;;
let fermeture_transitive m =
let résultat =
Array.make_matrix (nb_lignes m) (nb_colonnes m) 0 in
for i = 0 to nb_lignes m - 1 do
for j = 0 to nb_colonnes m - 1 do
résultat.(i).(j) <- m.(i).(j)
done
done;
for x = 0 to nb_colonnes m - 1 do
phi résultat x done;
résultat;; |
(* Tableaux de successeurs *)
type graphe_point = (int list) array;;
let omega = -1;;
let succ_of_mat m =
let nb_max_succ = ref 0 in
for i = 0 to nb_lignes m - 1 do
nb_max_succ := 0;
for j = 0 to nb_colonnes m - 1 do
if m.(i).(j) = 1 then
nb_max_succ := max j !nb_max_succ
done;
done;
let succ =
Array.make_matrix (nb_lignes m) (!nb_max_succ + 1) 0 in
let k = ref 0 in
for i = 0 to nb_lignes m - 1 do
k := 0;
for j = 0 to nb_colonnes m - 1 do
if m.(i).(j) = 1 then begin
succ.(i).(!k) <- j;
incr k
end
done;
succ.(i).(!k) <- omega
done;
succ;; |
(* Listes de successeurs *)
let liste_succ_of_mat m =
let gpoint = Array.make (nb_colonnes m) [] in
for i = 0 to nb_lignes m - 1 do
for j = 0 to nb_colonnes m - 1 do
if m.(i).(j) = 1
then gpoint.(i) <- j :: gpoint.(i)
done
done;
gpoint;; |
let numéro = Array.make (Array.length succ) (-1);;
let num = ref (-1);;
let rec num_prefixe k = begin
incr num;
numéro.(k) <- !num;
List.iter
(function x -> if numéro.(x) = -1 then
num_prefixe (x))
succ.(k)
end;;
let numPrefixe() = begin
Array.iter
(function x -> if numéro.(x) = -1 then
num_prefixe (x))
numéro
end;; |
let num_largeur k =
let f = file_vide() in begin
fajouter k f;
while not (fvide q) do
let k = fvaleur(f) in begin
fsupprimer f;
incr num;
numéro.(k) <- !num;
List.iter
(function x -> if numéro.(x) = -1 then
begin
fajouter x f;
numéro.(x) <- 0
end)
succ.(k)
end
done
end;;
let numLargeur() = begin
Array.iter
(function x -> if numéro.(x) = -1 then
num_largeur (x))
numéro
end;; |
(* calcule la composante connexe
de k et retourne son point d'attache *)
let rec comp_connexe k = begin
incr num; numéro.(k) <- !num;
Pile.ajouter k p;
let min = ref !num in begin
List.iter
(function x ->
let m = if numéro.(x) = -1 then
comp_connexe (x)
else
numéro.(x)
in if m < !min then
min := m)
succ.(k);
if !min = numéro.(k) then
(try while true do
printf "%d " (Pile.sommet p);
numéro.(Pile.sommet p) <- max_int;
Pile.supprimer p;
if (Pile.sommet p) = k then raise Exit
done
with Exit -> printf "\n");
!min
end
end;;
let compConnexe() = begin
Array.iter
(function x -> if numéro.(x) = -1 then
comp_connexe (x))
numéro
end;; |








