
| Figure 5.1: Un arbre binaire portant des informations aux nœuds. |



Dans ce chapitre, nous traitons d’abord les arbres binaires de recherche, puis les arbres équilibrés.
Un arbre binaire qui n’est pas vide est formé d’un nœud, sa racine, et de deux sous-arbres binaires, l’un appelé le fils gauche, l’autre le fils droit. Nous nous intéressons aux arbres contenant des informations. Chaque nœud porte une information, appelée son contenu. Un arbre non vide est donc entièrement décrit par le triplet (fils gauche, contenu de la racine, fils droit). Cette définition récursive se traduit en une spécification de programmation. Il suffit de préciser la nature du contenu d’un nœud. Pour simplifier, nous supposons que le contenu est un entier. On obtient alors la définition.
class Arbre
{
int contenu;
Arbre filsG, filsD;
Arbre(Arbre g, int c, Arbre d)
{
filsG = g;
contenu = c;
filsD = d;
}
}
L’arbre vide est, comme d’habitude, représenté par null. Un arbre réduit à une feuille, de contenu x, est créé par
new Arbre(null, x, null)
L’arbre de la figure 5.1 est créé par
new Arbre(
new Arbre(
new Arbre(null, 3, null),
5,
new Arbre(
new Arbre(
new Arbre(null, 6, null),
8,
null)
12,
new Arbre(null, 13, null))),
20,
new Arbre(
new Arbre(null, 21, null),
25,
new Arbre(null, 28, null)))

Figure 5.1: Un arbre binaire portant des informations aux nœuds.
Avant de poursuivre, reprenons le schéma déjà utilisé pour les listes. Quatre fonctions caractérisent les arbres: composer, cle, filsGauche, filsDroit. Elles s’implantent facilement:
static Arbre composer(Arbre g, int c, Arbre d)
{
return new Arbre(g, c, d);
}
static int cle(Arbre a)
{
return a.contenu;
}
static Arbre filsGauche(Arbre a)
{
return a.filsG;
}
static Arbre filsDroit(Arbre a)
{
return a.filsD;
}
Les quatre fonctions sont liées par les équations suivantes:
|
Comme pour les listes, ces quatre fonctions sont à la base d’opérations non destructives.
La définition récursive des arbres binaires conduit naturellement à une programmation récursive, comme pour les listes. Voici quelques exemples: la taille d’un arbre, c’est-à-dire le nombre t(a) de ses nœuds, s’obtient par la formule
| t(a) = |
|
où sont notés ag et ad les sous-arbres gauche et droit de a. D’où la méthode
static int taille(Arbre a)
{
if (a == null)
return 0;
return 1 + taille(a.filsG) + taille(a.filsD);
}
Des formules semblables donnent le nombre de feuilles ou la hauteur d’un arbre. Nous illustrons ce style de programmation par les parcours d’arbre définis page ??. Les trois parcours en profondeur s’écrivent:
static void parcoursPréfixe(Arbre a)
{
if (a == null)
return;
System.out.print(a.contenu + " ");
parcoursPréfixe(a.filsG);
parcoursPréfixe(a.filsD);
}
static void parcoursInfixe(Arbre a)
{
if (a == null)
return;
parcoursInfixe(a.filsG);
System.out.print(a.contenu + " ");
parcoursInfixe(a.filsD);
}
static void parcoursSuffixe(Arbre a)
{
if (a == null)
return;
parcoursSuffixe(a.filsG);
parcoursSuffixe(a.filsD);
System.out.print(a.contenu + " ");
}
Le parcours en largeur d’un arbre binaire s’écrit simplement avec une file. Le parcours préfixe s’écrit lui aussi simplement de manière itérative, avec une pile. Nous reprenons les classes Pile et File du chapitre 1, sauf que ce sont, cette fois-ci, des piles ou des files d’arbres. On écrit alors
static void parcoursPréfixeI(Arbre a)
{
if (a == null)
return;
Pile p = new Pile();
p.ajouter(a);
while (!p.estVide())
{
a = p.valeur();
p.supprimer();
System.out.print(a.contenu + " ");
if (a.filsD != null)
p.ajouter(a.filsD);
if (a.filsG != null)
p.ajouter(a.filsG);
}
}
static void parcoursLargeurI(Arbre a)
{
if (a == null)
return;
File f = new File();
f.ajouter(a);
while (!f.estVide())
{
a = f.valeur();
f.supprimer();
System.out.print(a.contenu + " ");
if (a.filsG != null)
f.ajouter(a.filsG);
if (a.filsD != null)
f.ajouter(a.filsD);
}
}
Rappelons qu’un arbre est ordonné si la suite des fils de chaque nœud est ordonnée. Il est donc naturel de représenter les fils dans une liste chaînée. Un nœud contient aussi la référence à son fils aîné, c’est-à-dire à la tête de la liste de ses fils. Ainsi, chaque nœud contient deux références, celle à son fils aîné, et celle à son frère cadet. En d’autres termes, la structure des arbres binaires convient parfaitement, sous réserve de rebaptiser filsAine le champ filsG et frereCadet le champ filsD.
class ArbreOrdonne
{
int contenu;
Arbre filsAine, frereCadet;
Arbre(Arbre g, int c, Arbre d)
{
filsAine = g;
contenu = c;
frereCadet = d;
}
}
Cette représentation est aussi appelée « fils gauche — frère droit » (voir figure 5.2).
Figure 5.2: Représentation d’un arbre ordonné par un arbre binaire.
Noter que la racine de l’arbre binaire n’a pas de fils droit. En fait, cette représentation s’étend à la représentation, par un seul arbre binaire, d’une forêt ordonnée d’arbres ordonnés.
Les arbres binaires servent à gérer des informations. Chaque nœud contient une donnée prise dans un certain ensemble. Nous supposons dans cette section que cet ensemble est totalement ordonné. Ceci est le cas par exemple pour les entiers et pour les mots.
Un arbre binaire a est un arbre binaire de recherche si, pour tout nœud s de a, les contenus des nœuds du sous-arbre gauche de s sont strictement inférieurs au contenu de s, et que les contenus des nœuds du sous-arbre droit de s sont strictement supérieurs au contenu de s (cf. figure 5.3).

Figure 5.3: Un arbre binaire de recherche.
Une petite mise en garde: contrairement à ce que l’analogie avec les tas pourrait laisser croire, il ne suffit pas de supposer que, pour tout nœud s de l’arbre, le contenu du fils gauche de s soit strictement inférieur au contenu de s, et que le contenu du fils droit de s soit supérieur au contenu de s. Ainsi, dans l’arbre de la figure 5.3, si on change la valeur 13 en 11, on n’a plus un arbre de recherche...
Une conséquence directe de la définition est la règle suivante:
Règle. Dans un arbre binaire de recherche,
le parcours infixe fournit les contenus des nœuds en ordre croissant.
Une seconde règle permet de déterminer dans certains cas le nœud qui précède un nœud donné dans le parcours infixe.
Règle. Si un nœud possède un fils gauche,
son prédécesseur dans le parcours infixe est le nœud le plus à droite dans
son sous-arbre gauche. Ce nœud n’est pas nécessairement une
feuille, mais il n’a pas de fils droit.
Ainsi, dans l’arbre de la figure 5.3, la racine possède un fils gauche, et son prédécesseur est le nœud de contenu 14, qui n’a pas de fils droit...
Les arbres binaires de recherche fournissent, comme on le verra, une implantation souvent efficace d’un type abstrait de données, appelé dictionnaire, qui opère sur un ensemble totalement ordonné à l’aide des opérations suivantes:
Le dictionnaire est simplement une table d’associations (chapitre 3) dont les informations sont inexistantes. Plusieurs implantations d’un dictionnaire sont envisageables: par tableau, par liste ordonnés ou non, par tas, et par arbre binaire de recherche. La table 5.1 rassemble la complexité des opérations de dictionnaire selon la structure de données choisie.
Tableau 5.1: Complexité des implantations de dictionnaires
L’entier h désigne la hauteur de l’arbre. On voit que lorsque l’arbre est bien équilibré, c’est-à-dire lorsque la hauteur est proche du logarithme de la taille, les opérations sont réalisables de manière particulièrement efficace.
Nous commençons l’implantation des opérations de dictionnaire sur les arbres binaires de recherche par l’opération la plus simple, la recherche. Plutôt que d’écrire une méthode booléenne qui teste la présence d’un élément dans l’arbre, nous écrivons une méthode qui retourne l’arbre dont la racine porte l’élément cherché s’il figure dans l’arbre, et null sinon. Comme toujours, il y a le choix entre une méthode récursive, calquée sur la définition récursive des arbres, et une méthode itérative, cheminant dans l’arbre. Nous présentons les deux, en commençant par la méthode récursive. Pour chercher si un élément x figure dans un arbre A, on commence par comparer x au contenu c de la racine de A. S’il y a égalité, on a trouvé la réponse; sinon il y a deux cas selon que x<c et x>c. Si x<c, alors x figure peut-être dans le sous-arbre gauche Ag de A, mais certainement pas dans le sous-arbre droit Ad. On élimine ainsi de la recherche tous les nœuds du sous-arbre droit. Cette méthode n’est pas sans rappeler la recherche dichotomique. La méthode s’écrit récursivement comme suit:
static Arbre chercher(int x, Arbre a)
{
if (a == null || x == a.contenu)
return a;
if (x < a.contenu)
return chercher(x, a.filsG);
return chercher(x, a.filsD);
}
Cette méthode retourne null si l’arbre a ne contient pas x. Ceci inclut le cas où l’arbre est vide. Voici la méthode itérative.
static chercherI(int x, Arbre a)
{
while(a != null && x != a.contenu)
if (x < a.contenu)
a = a.filsG;
else
a = a.filsD;
return a;
}
On voit que la condition de continuation dans la méthode itérative chercherI est la négation de la condition d’arrêt de la méthode récursive, ce qui est logique.
L’adjonction d’un nouvel élément à un arbre modifie l’arbre. Nous sommes confrontés au même choix que pour les listes: soit on construit une nouvelle version de l’arbre (version non destructive), soit on modifie l’arbre existant (version destructive). Nous présentons une méthode récursive dans les deux versions. Dans les deux cas, si l’entier figure déjà dans l’arbre, on ne l’ajoute pas une deuxième fois. Voici la version destructive.
static Arbre inserer(int x, Arbre a)
{
if (a == null)
return new Arbre(null, x, null);
if (x < a.contenu)
a.filsG = inserer(x, a.filsG);
else if (x > a.contenu)
a.filsD = inserer(x, a.filsD);
return a;
}
Voici la version non destructive.
static Arbre inserer(int x, Arbre a)
{
if (a == null)
return new Arbre(null, x, null);
if (x < a.contenu)
{
Arbre b = inserer(x, a.filsG);
return new Arbre(b, a.contenu, a.filsD);
}
else if (x > a.contenu)
{
Arbre b = inserer(x, a.filsD);
return new Arbre(a.filsG, a.contenu, b);
}
return a;
}
La suppression d’une clé dans un arbre est une opération plus complexe. Elle s’accompagne de la suppression d’un nœud. Comme on le verra, ce n’est pas toujours le nœud qui porte la clé à supprimer qui sera enlevé. Soit s le nœud qui porte la clé x à supprimer. Trois cas sont à considérer selon le nombre de fils du nœud x:
La suppression de la feuille qui porte la clé 13 est illustrée dans la figure 5.4

Figure 5.4: Suppression de la clé 13 par élimination d’une feuille.
La figure 5.5 illustre la « remontée »: le nœud s qui porte la clé 16 n’a qu’un seul enfant. Cet enfant devient l’enfant du père de s, le nœud de clé 20.
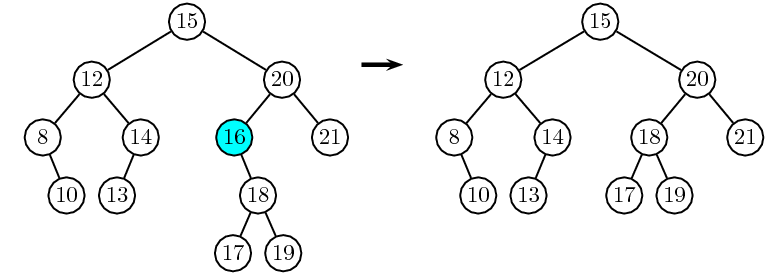
Figure 5.5: Suppression de la clé 16 par remontée du fils.
Le cas d’un nœud à deux fils est illustré dans la figure 5.6. La clé à supprimer se trouve à la racine de l’arbre. On ne supprime pas le nœud, mais seulement sa clé, en remplaçant la clé par une autre clé. Pour conserver l’ordre sur les clés, il n’y a que deux choix : la clé du prédécesseur dans l’ordre infixe, ou la clé du successeur. Nous choisissons la première solution. Ainsi, la clé 14 est mise à la racine de l’arbre. Nous sommes alors ramenés au problème de la suppression du nœud du prédécesseur et de sa clé. Comme le prédécesseur est le nœud le plus à droite du sous-arbre gauche, il n’a pas de fils droit, donc il a zéro ou un fils, et sa suppression est couverte par les deux premiers cas.

Figure 5.6: Suppression de la clé 15 par substitution de la clé 14 et suppression de ce nœud.
Trois méthodes coopèrent pour la suppression. La première, suppression, recherche le nœud portant la clé à supprimer; la deuxième, suppressionRacine, effectue la suppression selon les cas énumérés ci-dessus. La troisième, dernierDescendant est une méthode auxiliaire; elle calcule le précédesseur d’un nœud qui a un fils gauche.
static Arbre supprimer(int x, Arbre a)
{
if (a == null)
return a;
if (x == a.contenu)
return supprimerRacine(a);
if (x < a.contenu)
a.filsG = supprimer(x, a.filsG);
else
a.filsD = supprimer(x, a.filsD);
return a;
}
La méthode suivante supprime la clé de la racine de l’arbre.
static Arbre supprimerRacine(Arbre a)
{
if (a.filsG == null)
return a.filsD;
if (a.filsD == null)
return a.filsG;
Arbre f = dernierDescendant(a.filsG);
a.contenu = f.contenu;
a.filsG = supprimer(f.contenu, a.filsG);
}
La dernière méthode est toute simple:
static Arbre dernierDescendant(Arbre a)
{
if (a.filsD == null)
return a;
return dernierDescendant(a.filsD);
}
La récursivité croisée entre les méthodes supprimer et supprimerRacine est déroutante au premier abord. En fait, l’appel à supprimer à la dernière ligne de supprimerRacine conduit au nœud prédécesseur de la racine de l’arbre, appelé f. Comme ce nœud n’a pas deux fils, il n’appelle pas une deuxième fois la méthode supprimerRacine...
Il est intéressant de voir une réalisation itérative de la suppression. Elle démonte entièrement la « mécanique » de l’algorithme. En fait, chacune des trois méthodes peut séparément être écrite de façon récursive.
static Arbre supprimer(int x, Arbre a)
{
Arbre b = a;
while (a != null && x != a.contenu)
if (x < a.contenu)
a = a.filsG;
else
a = a.filsD;
if (a != null)
a = supprimerRacine(a);
return b;
}
Voici la deuxième.
static Arbre supprimerRacine(Arbre a)
{
if (a.filsG == null)
return a.filsD;
if (a.filsD == null)
return a.filsG;
Arbre b = a.filsG;
if (b.filsD == null)
{ // cas (i)
a.contenu = b.contenu;
a.filsG = b.filsG;
}
else
{ // cas (ii)
Arbre p = avantDernierDescendant(b);
Arbre f = p.filsD;
a.contenu = f.contenu;
p.filsD = f.filsG;
}
return a;
}
Et voici le calcul de l’avant-dernier descendant:
static Arbre avantDernierDescendant(Arbre a)
{
while (a.filsD.filsD != null)
a = a.filsD;
return a;
}
Décrivons plus précisément le fonctionnement de la méthode supprimerRacine. La première partie permet de se ramener au cas où la racine de l’arbre a a deux fils. On note b le fils gauche de a, et pour déterminer le prédécesseur de la racine de a, on cherche le nœud le plus à droite dans l’arbre b. Deux cas peuvent se produire :
Les deux cas sont illustrés sur les figures 5.7 et 5.8.

Figure 5.7: Suppression de la racine, version itérative, cas (i).
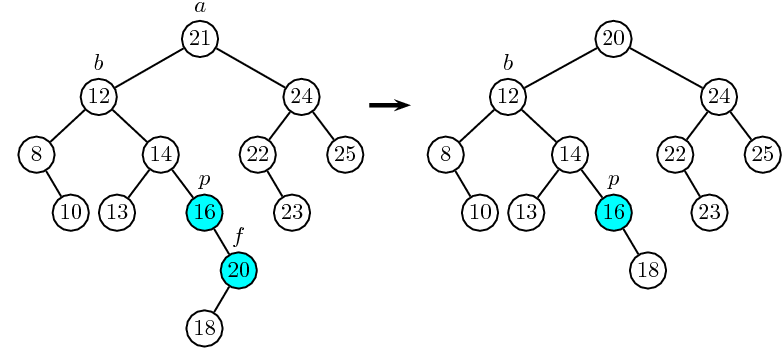
Figure 5.8: Suppression de la racine, version itérative, cas (ii).
Dans le premier cas, la clé de la racine de b est transférée à la racine de a, et b est remplacée par son sous-arbre gauche (qui peut d’ailleurs être vide). Dans le deuxième cas, on cherche l’avant-dernier descendant, noté p, de b sur la branche droite de b, au moyen de la méthode avantDernierDescendant. Cela peut être b lui-même, ou un de ses descendants (notons que dans le cas (i), l’avant-dernier descendant n’existe pas, ce qui explique le traitement séparé opéré dans ce cas). Le sous-arbre droit f de p n’est pas vide par définition. La clé de f est transférée à la racine de a, et f est remplacé par son sous-arbre gauche — ce qui fait disparaître la racine de f.
Il est facile de constater, sur nos implantations, que la recherche, l’insertion et la suppression dans un arbre binaire de recherche se font en complexité O(h), où h est la hauteur de l’arbre. Le cas le pire, pour un arbre à n nœuds, est O(n). En ce qui concerne la hauteur moyenne, deux cas sont à considérer. La première des propositions s’applique aux arbres, la deuxième aux permutations.
La différence provient du fait que plusieurs permutations peuvent donner le même arbre. Par exemple les permutations 2, 1, 3 et 2, 3, 1 produisent toutes les deux l’arbre de la figure 5.9.
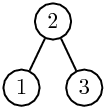
Figure 5.9: L’arbre produit par la suite d’insertions 2,1,3, ou par la suite 2,3,1.
Comme nous l’avons déjà constaté, les coûts de la recherche, de l’insertion et de la suppression dans un arbre binaire de recherche sont de complexité O(h), où h est la hauteur de l’arbre. Le cas le pire, pour un arbre à n nœuds, est O(n). Ce cas est atteint par des arbres très déséquilibrés, ou « filiformes ». Pour éviter que les arbres puissent prendre ces formes, on utilise des opérations plus ou moins simples, mais peu coûteuses en temps, de transformation d’arbres. À l’aide de ces transformations on tend à rendre l’arbre le plus régulier possible dans un sens qui est mesuré par un paramètre dépendant en général de la hauteur. Une famille d’arbres satisfaisant une condition de régularité est appelée une famille d’arbres équilibrés. Plusieurs espèces de tels arbres ont été développés, notamment les arbres AVL, les arbres 2-3, les arbres rouge et noir, ainsi qu’une myriade de variantes. Dans les langages comme Java ou C++, des modules de gestion d’ensembles sont préprogrammés. Lorsqu’un ordre total existe sur les éléments de ces ensembles, ils sont en général gérés, en interne, par des arbres rouge et noir.
La famille des arbres AVL est nommée ainsi d’après leurs inventeurs, Adel’son-Velskii et Landis, qui les ont présentés en 1962. Au risque de paraître vieillots, nous décrivons ces arbres plus en détail parce que leur programmation peut être menée jusqu’au bout, et parce que les principes utilisés dans leur gestion se retrouvent dans d’autres familles plus complexes.
Un arbre binaire est un arbre AVL si, pour tout nœud de l’arbre, les hauteurs des sous-arbres gauche et droit diffèrent d’au plus 1.
Rappelons qu’une feuille est un arbre de hauteur 0, et que l’arbre vide a la hauteur −1. L’arbre vide, et l’arbre réduit à une feuille, sont des arbres AVL.
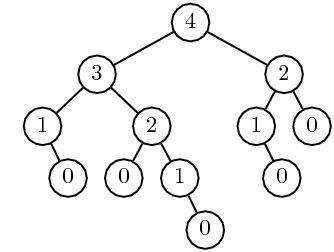
Figure 5.10: Un arbre AVL, avec les hauteurs aux nœuds.
L’arbre de la figure 5.10 porte, dans chaque nœud, la hauteur de son sous-arbre.
Un autre exemple est fourni par les arbres de Fibonacci, qui sont des arbres binaires An tels que les sous-arbres gauche et droit de An sont respectivement An−1 et An−2. Les premiers arbres de Fibonacci sont donnés dans la figure 5.11.

Figure 5.11: Les premiers arbres de Fibonacci.
L’intérêt des arbres AVL résulte du fait que leur hauteur est toujours logarithmique en fonction de la taille de l’arbre. En d’autres termes, la recherche, l’insertion et la suppression (sous réserve d’un éventuel rééquilibrage) se font en temps logarithmique. Plus précisément, on a la propriété que voici.
| log2(1+n) ≤ 1+h ≤ αlog2(2+n) |
| N(h)= 1 + N(h−1) + N(h−2) |
| F(h)= |
| (Φh+3 − Φ−(h+3)) |
Par exemple, pour un arbre AVL qui a 100000 nœuds, la hauteur est comprise entre 17 et 25. C’est le nombre d’opérations qu’il faut donc pour rechercher, insérer ou supprimer une donnée dans un tel arbre.
Nous introduisons maintenant une opération sur les arbres appelée rotation. Les rotations sont illustrées sur la figure 5.12. Soit A=(B,q,W) un arbre binaire tel que B=(U,p,V). La rotation gauche est l’opération
| ( (U,p,V), q, W) → (U,p,(V, q, W)) |
et la rotation droite est l’opération inverse. Les rotations gauche (droite) ne sont donc définies que pour les arbres binaires non vides dont le sous-arbre gauche (resp. droit) n’est pas vide.
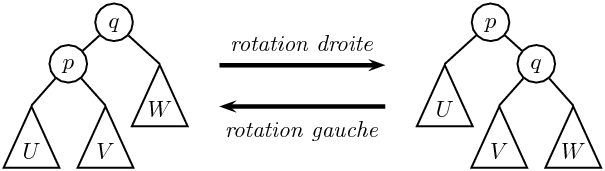
Figure 5.12: Rotation.
Remarquons en passant que pour l’arbre d’une expression arithmétique, si les symboles d’opération p et q sont les mêmes, les rotations expriment que l’opération est associative.
Les rotations ont la propriété de pouvoir être implantées en temps constant (voir ci-dessous), et de préserver l’ordre infixe. En d’autres termes, si A est un arbre binaire de recherche, tout arbre obtenu à partir de A par une suite de rotations gauche ou droite d’un sous-arbre de A reste un arbre binaire de recherche. En revanche, comme le montre la figure 5.13, la propriété AVL n’est pas conservée par rotation.
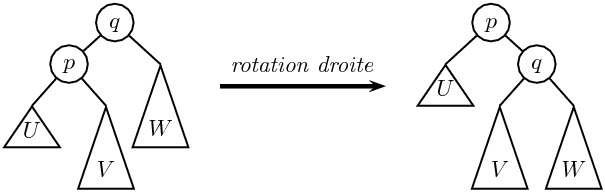
Figure 5.13: Les rotations ne préservent pas la propriété AVL.
Pour remédier à cela, on considère une double rotation qui est en fait composée de deux rotations. La figure 5.14 décrit une double rotation droite, et montre comment elle est composée d’une rotation gauche du sous-arbre gauche suivie d’un rotation droite. Plus précisément, soit A= ((U, p, (V, q, W)), r, X) un arbre dont le sous-arbre gauche possède un sous-arbre droit. La double rotation droite est l’opération
| A= ((U, p, (V, q, W)), r, X)→ A′=((U,p,V),q,(W,r,X)) |
Vérifions qu’elle est bien égale à la composition de deux rotations. D’abord, une rotation gauche de B = (U, p, (V, q, W)) donne B′ = ((U, p, V), q, W), et l’arbre A=(B,r,X) devient A″=(B′,r,X); la rotation droite de A″ donne en effet A′. On voit qu’une double rotation droite diminue la hauteur relative des sous-arbres V et W, et augmente celle de X. La double rotation gauche est définie de manière symétrique.
Figure 5.14: Rotations doubles.
Voici une implantation non destructive d’une rotation gauche.
static Arbre rotationG(Arbre a) // non destructive
{
Arbre b = a.filsD;
Arbre c = new Arbre(a.filsG, a.contenu, b.filsG);
return new Arbre(c, b.contenu, b.filsD);
}
La fonction suppose que le sous-arbre gauche, noté b, n’est pas vide. La rotation gauche destructive est aussi simple à écrire.
static Arbre rotationG(Arbre a) // destructive
{
Arbre b = a.filsD;
a.filsD = b.filsG;
b.filsG = a;
return b;
}
Les double rotations s’écrivent par composition.
L’insertion et la suppression dans un arbre AVL peuvent transformer l’arbre en un arbre qui ne satisfait plus la contrainte sur les hauteurs. Dans la figure 5.15, un nœud portant l’étiquette 50 est inséré dans l’arbre de gauche. Après insertion, on obtient l’arbre du milieu qui n’est plus AVL. Une double rotation autour de la racine suffit à rééquilibrer l’arbre.

Figure 5.15: Insertion suivie d’une double rotation.
Cette propriété est générale. Après une insertion (respectivement une suppression), il suffit de rééquilibrer l’arbre par des rotations ou double rotations le long du chemin qui conduit à la feuille où l’insertion (respectivement la suppression) a eu lieu. L’algorithme est le suivant:
Algorithme. Soit A un arbre, G et D
ses sous-arbres gauche et droit. On suppose que |h(G)−h(D)|=2. Si
h(G)−h(D)=2, on fait une rotation droite, mais précédée d’une rotation
gauche de G si h(g) < h(d) (on note g et d les sous-arbres gauche
et droit de G). Si h(G)−h(D) = −2 on opère de façon symétrique.
On peut montrer en exercice qu’il suffit d’une seule rotation ou double rotation pour rééquilibrer un arbre AVL après une insertion. Cette propriété n’est plus vraie pour une suppression.
Pour l’implantation, nous munissons chaque nœud d’un champ supplémentaire qui contient la hauteur de l’arbre dont il est racine. Pour une feuille par exemple, ce champ a la valeur 0. Pour l’arbre vide, qui est représenté par null et qui n’est donc pas un objet, la hauteur vaut −1. La méthode H sert à simplifier l’accès à la hauteur d’un arbre.
class Avl
{
int contenu;
int hauteur;
Avl filsG, filsD;
Avl(Avl g, int c, Avl d)
{
filsG = g;
contenu = c;
filsD = d;
hauteur = 1 + Math.max(H(g),H(d));
}
static int H(Avl a)
{
return (a == null) ? -1 : a.hauteur;
}
static void calculerHauteur(Avl a)
{
a.hauteur = 1 + Math.max(H(a.filsG), H(a.filsD));
}
...
}
La méthode calculerHauteur recalcule la hauteur d’un arbre à partir des hauteurs de ses sous-arbres. L’usage de H permet de traiter de manière unifiée le cas où l’un de ses sous-arbres serait l’arbre vide. Les rotations sont reprises de la section précédente. On utilise la version non destructive qui réévalue la hauteur. Ces méthodes et les suivantes font toutes partie de la classe Avl.
static Avl rotationG(Avl a)
{
Avl b = a.filsD;
Avl c = new Avl(a.filsG, a.contenu, b.filsG);
return new Avl(c, b.contenu, b.filsD);
}
La méthode principale implante l’algorithme de rééquilibrage exposé plus haut.
static Avl equilibrer(Avl a)
{
a.hauteur = 1 + Math.max(H(a.filsG), H(a.filsD));
if(H(a.filsG) - H(a.filsD) == 2)
{
if (H(a.filsG.filsG) < H(a.filsG.filsD))
a.filsG = rotationG(a.filsG);
return rotationD(a);
} //else version symétrique
if (H(a.filsG) - H(a.filsD) == -2)
{
if (H(a.filsD.filsD) < H(a.filsD.filsG))
a.filsD = rotationD(a.filsD);
return rotationG(a);
}
return a;
}
Il reste à écrire les méthodes d’insertion et de suppression, en prenant soin de rééquilibrer l’arbre à chaque étape. On reprend simplement les méthodes déjà écrites pour un arbre binaire de recherche général. Pour l’insertion, on obtient
static Avl inserer(int x, Avl a)
{
if (a == null)
return new Avl(null, x, null);
if (x < a.contenu)
a.filsG = inserer(x, a.filsG);
else if (x > a.contenu)
a.filsD = inserer(x, a.filsD);
return equilibrer(a); //seul changement
}
La suppression s’écrit comme suit
static Avl supprimer(int x, Avl a)
{
if (a == null)
return a;
if (x == a.contenu)
return supprimerRacine(a);
if (x < a.contenu)
a.filsG = supprimer(x, a.filsG);
else
a.filsD = supprimer(x, a.filsD);
return equilibrer(a); // seul changement
}
static Avl supprimerRacine(Avl a)
{
if (a.filsG == null && a.filsD == null)
return null;
if (a.filsG == null)
return equilibrer(a.filsD);
if (a.filsD == null)
return equilibrer(a.filsG);
Avl b = dernierDescendant(a.filsG);
a.contenu = b.contenu;
a.filsG = supprimer(a.contenu, a.filsG);
return equilibrer(a); // seul changement
}
static Avl dernierDescendant(Avl a) // inchangée
{
if (a.filsD == null)
return a;
return dernierDescendant(a.filsD);
}
Dans cette section, nous décrivons de manière succinte les arbres a-b. Il s’agit d’une des variantes d’arbres équilibrés qui ont la propriété que toutes leurs feuilles sont au même niveau, les nœuds internes pouvant avoir un nombre variable de fils (ici entre a et b). Dans cette catégorie d’arbres, on trouve aussi les B-arbres et en particulier les arbres 2-3-4. Les arbres rouge et noir (ou bicolores) sont semblables.
L’intérêt des arbres équilibrés est qu’ils permettent des modifications en temps logarithmique. Lorsque l’on manipule de très grands volumes de données, il survient un autre problème, à savoir l’accès proprement dit aux données. En effet, les données ne tiennent pas en mémoire vive, et les données sont donc accessibles seulement sur la mémoire de masse, un disque en général. Or, un seul accès disque peut prendre, en moyenne, environ autant de temps que 200 000 instructions. Les B-arbres ou les arbres a-b servent, dans ce contexte, à minimiser les accès au disque.
Un disque est divisé en pages (par exemple de taille 512, 2048, 4092 ou 8192 octets). La page est l’unité de transfert entre mémoire centrale et disque. Il est donc rentable de grouper les données par blocs, et de les manipuler de concert.
Les données sont en général repérées par des clés, qui sont rangées dans un arbre. Si chaque accès à un nœud requiert un accès disque, on a intérêt à avoir des nœuds dont le nombre de fils est voisin de la taille d’une page. De plus, la hauteur d’un tel arbre — qui mesure le nombre d’accès disques nécessaire — est alors très faible. En effet, si chaque nœud a de l’ordre de 1000 fils, il suffit d’un arbre de hauteur 3 pour stocker un milliard de clés.
Nous considérons ici des arbres de recherche qui ne sont plus binaires, mais d’arité plus grande. Chaque nœud interne d’un tel arbre contient, en plus des références vers ses sous-arbres, des balises, c’est-à-dire des valeurs de clé qui permettent de déterminer le sous-arbre où se trouve l’information cherchée. Plus précisément, si un nœud interne possède d+1 sous-arbres A0, …, Ad, alors il est muni de d balises k1, …, kd telles que
| c0 ≤ k1 < c1 ≤ ⋯ ≤ kd<cd |
pour toute séquence de clés (c0,…, cd), où chaque ci est une clé du sous-arbre Ai (cf. figure 5.16).
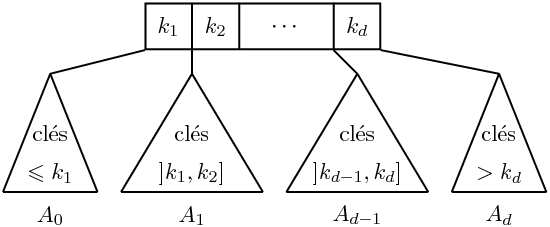
Figure 5.16: Un nœud interne muni de balises et ses sous-arbres.
Il en résulte que pour chercher une clé c, on détermine le sous-arbre Ai approprié en déterminant lequel des intervalles ]−∞, k1], ]k1,k2],…,]kd−1,kd], ]kd,∞[ contient la clé.
Soient a≥ 2 et b≥ 2a−1 deux entiers. Un arbre a-b est un arbre de recherche tel que
Les arbres 2-3 sont les arbres obtenus quand a et b prennent leurs valeurs minimales: tout nœud interne a alors 2 ou 3 fils.
Les B-arbres sont comme les arbres a-b avec b=2a−1 mais avec une interprétation différente : les informations sont aussi stockées aux nœuds internes, alors que, dans les arbres que nous considérons, les clés aux nœuds internes ne servent qu’à la navigation.
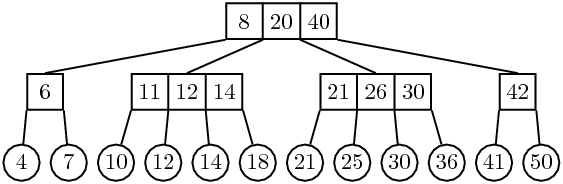
Figure 5.17: Un arbre 2-4. Un nœud a entre 2 et 4 fils.
L’arbre de la figure 5.17 représente un arbre 2-4. Les nœuds internes contiennent les balises, et les feuilles contiennent les clés. L’intérêt des arbres a-b est justifié par la proposition suivante.
| logn / logb ≤ h < 1 + log(n/2) / loga . |
Il résulte de la proposition précédente que la hauteur d’un arbre a-b ayant n feuilles est en O(logn). La complexité des algorithmes décrit ci-dessous (insertion et suppression) sera donc elle aussi en O(logn).
La recherche dans un arbre a-b repose sur le même principe que celle utilisée pour les arbres binaires de recherche: on parcourt les balises du nœud courant pour déterminer le sous-arbre dans lequel il faut poursuivre la recherche. Pour l’insertion, on commence par déterminer, par une recherche, l’emplacement de la feuille où l’insertion doit avoir lieu. On insère alors une nouvelle feuille, et une balise appropriée: la balise est la plus petite valeur de la clé à insérer et de la clé à sa droite.
Reste le problème du rééquilibrage qui se pose lorsque le nombre de fils d’un nœud dépasse le nombre autorisé. Si un nœud a b+1 fils, alors il est éclaté en deux nœuds qui se partagent les fils de manière équitable: le premier nœud reçoit les ⌊ (b+1)/2⌋ fils de gauche, le deuxième les fils de droite. Noter que b+1≥ 2a, et donc chaque nouveau nœud aura au moins a fils. Les balises sont également partagées, et la balise centrale restante est transmise au nœud père, pour qu’il puisse à son tour procéder à l’insertion des deux fils à la place du nœud éclaté.
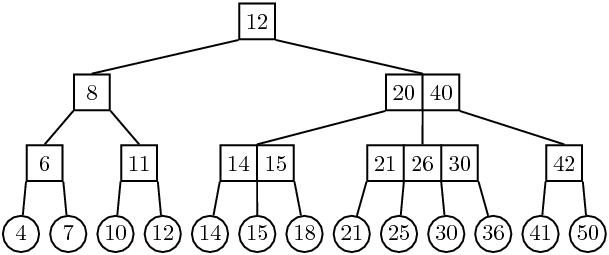
Figure 5.18: Un arbre 2-4. Un nœud a entre 2 et 4 fils.
L’insertion de la clé 15 dans l’arbre 5.17 produit l’arbre de la figure 5.18. Cette insertion se fait par un double éclatement. D’abord, le nœud aux balises 11, 12, 14 de l’arbre 5.17 est éclaté en deux. Mais alors, la racine de l’arbre 5.17 a un nœud de trop. La racine elle-même est éclatée, ce qui fait augmenter la hauteur de l’arbre.
Il est clair que l’insertion d’une nouvelle clé peut au pire faire éclater les nœuds sur le chemin de son lieu d’insertion à la racine — et la racine elle-même. Le coût est donc borné logarithmiquement en fonction du nombre de feuilles dans l’arbre.
Comme d’habitude, la suppression est plus complexe. Il s’agit de fusionner un nœud avec un nœud frère lorsqu’il n’a plus assez de fils, c’est-à-dire si son nombre de fils descend au dessous de a. Mais si son frère (gauche ou droit) a beaucoup de fils, la fusion des deux nœuds risque de conduire à un nœud qui a trop de fils et qu’il faut éclater. On groupe ces deux opérations sous la forme d’un partage (voir figure 5.19).
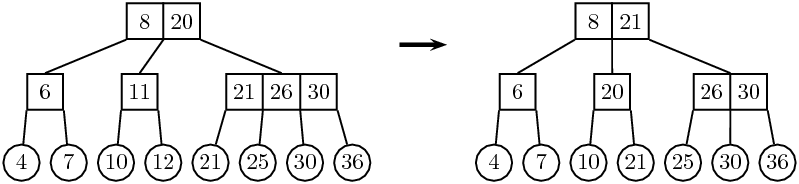
Figure 5.19: La suppression de 12 est absorbée par un partage.
Plus précisément, l’algorithme est le suivant:
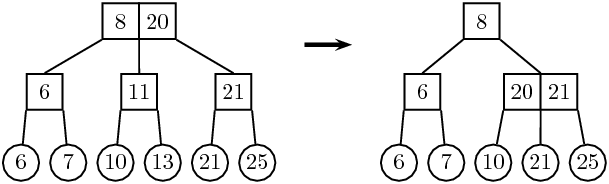
Figure 5.20: La suppression de 13 entraîne la fusion des deux nœuds de droite.
Là encore, le coût est majoré par un logarithme du nombre de feuilles. Il faut noter qu’il s’agit du comportement dans le cas le plus défavorable. On peut en effet démontrer
Ceci signifie donc qu’en moyenne, 1,5 opérations suffisent pour rééquilibrer l’arbre, et ce, quel que soit sa taille! Des résultats analogues valent pour des valeurs de a et b plus grandes.


