Chapitre 6  Expressions régulières

• Langages réguliers
• Notations supplémentaires
• Programmation avec les expressions régulières
• Implémentation des expressions régulières
• Une autre approche du filtrage

6.1  Langages réguliers

6.1.1  Les mots

On se donne un ensemble Σ de caractères, parfois dénommé alphabet. L’ensemble des mots sur Σ, noté Σ^*, est l’ensemble des suites finies de caractères. Un langage est un sous-ensemble de Σ^*, c’est-à-dire un ensemble particulier de mots.

Par exemple si Σ est l’ensemble des lettres usuelles, on peut définir le langage L₁ des mots français. Ou encore si Σ est l’ensemble des chiffres de 0 à 9, on peut définir le langage L₂ des représentations en base 10 des entiers naturels. Dans le premier cas, on peut tout simplement tenter de définir L₁ comme l’ensemble de tous les mots présents dans le dictionnaire de l’Académie française, dans le second cas, on peut recourir à une définition du style « un entier (décimal) est le chiffre zéro, ou une suite non vide de chiffres qui ne commence pas par zéro ». Les expressions régulières (ou rationnelles) sont une notation très commode pour définir des langages de mots du style de L₁ et L₂ ci-dessus.

Définissons tout de suite quelques notations sur les mots et les langages. Parmi les mots de Σ^* on distingue le mot vide noté є. Le mot vide est l’unique mot de longueur zéro. La concaténation de deux mots m₁ et m₂ est le mot obtenu en mettant m₁ à la fin de m₂. On note · l’opérateur de concaténation, mais on omet souvent cet opérateur et on note donc souvent la concaténation m₁ ·m₂ par une simple juxtaposition m₁m₂. La concaténation est une opération associative qui possède un élément neutre : le mot vide є. Dans l’écriture m = m₁m₂, m₁ est le préfixe du mot m, tandis que m₂ est le suffixe du mot m.

La concaténation s’étend naturellement aux ensembles de mots, on note L₁ · L₂ le langage obtenu en concaténant tous les mots de L₁ avec les mots de L₂.

Enfin on note L^⋆ le langage obtenu en concaténant les mots de L.

C’est-à-dire qu’un mot m de L^* est la concaténation de n mots (n ≥ 0) m₁, …m_n, où les m_i sont tous des mots de L.

6.1.2  Syntaxe des expressions régulières

Les expressions régulières ou motifs, notées p, sont définies ainsi :

• Le mot vide є est une expression régulière.
• Un caractère c (un élément de l’alphabet Σ) est une expression régulière.
• Si p₁ et p₂ sont des expressions régulières, alors l’alternative p₁|p₂ est une expression régulière.
• Si p₁ et p₂ sont des expressions régulières, alors la concaténation p₁·p₂ est une expression régulière.
• Si p est une expression régulière, alors la répétition p* est une expression régulière.

On reconnaît ici la définition d’un arbre, et même d’un arbre de syntaxe abstraite. Il y a deux sortes de feuilles, mot vide et caractères ; deux sortes de nœuds binaires, concaténation et alternative ; et une sorte de nœud unaire, la répétition. Comme d’habitude pour lever les ambiguïtés dans l’écriture linéaire d’un arbre, on a recours à des priorités (à savoir, la répétition est plus prioritaire que la concaténation, elle-même plus prioritaire que l’alternative) et à des parenthèses.

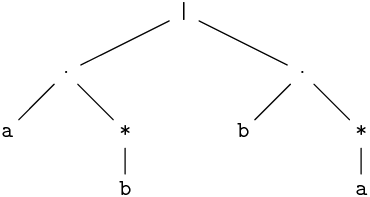
Ainsi, pour Σ = {a, b, c}, le motif ab*|ba* est à comprendre comme ((a)(b*))|((b)(a*)), ou plus informatiquement comme l’arbre de la figure 6.1.

---

Figure 6.1: L’arbre de syntaxe abstraite de l’expression ab*|ba*

---

Pour se souvenir des priorités adoptées on peut noter l’analogie avec les expressions arithmétiques : les opérations de concaténation et d’alternative ont les même priorités respectives que la multiplication et l’addition, enfin la répétition se comporte comme la mise à la puissance.

Dans ce polycopié nous exprimons les expressions régulières sous la forme « programme » et non pas d’expression mathématiques Concrètement, nous avons écrit ab*|ba* et non pas ab^⋆ ∣ ba^⋆. Ce parti pris entraîne que le motif vide ne peut plus être donné par є, si nécessaire nous le représenterons donc par exemple comme ().

Avec un peu d’habitude, on comprend nos écritures comme des arbres de syntaxe abstraites. Cela lève toutes les ambiguïtés d’entrée de jeu. On doit sans doute remarquer qu’en réalité, nos priorités ne lèvent pas toutes les ambiguïtés. En effet, on peut comprendre abc comme a(bc) ou comme (ab)c, c’est-à-dire comme l’arbre de gauche ou comme l’arbre de droite de la figure 6.2. Au fond cette ambiguïté n’a ici aucune importance, car l’opération de concaténation des mots est associative. Il en résulte que la concaténation des motifs est également associative.

---

Figure 6.2: Deux arbres possibles pour abc

---

Comme nous allons le voir immédiatement, il en va de même pour l’alternative.

6.1.3  Sémantique des expressions régulières

Une expression arithmétique a une valeur (plus généralement on dit aussi une sémantique) : c’est tout simplement l’entier résultat du calcul. De même, une expression régulière a une valeur qui est ici un ensemble de mots. Il est logique que la définition de la sémantique reprenne la structure de la définition des expressions régulières. C’est tout simplement une définition inductive, qui à chaque expression régulière p associe un sous-ensemble [[p]] de Σ^*.

Cette définition a le parfum usuel des définitions de sémantique, on a presque rien écrit en fait ! Tout a déjà été dit ou presque dans la section 6.1.1 sur les mots. Lorsque m appartient au langage défini par p, on dit aussi que le motif p filtre le mot m. Un langage qui peut être défini comme la valeur d’une expression régulière est dit langage régulier.

6.1.4  Filtrage

La relation de filtrage m ∈ [[p ]], également notée p ≼ m, peut être définie directement par les règles de la figure 6.3.

---

Figure 6.3: Définition de la relation p filtre m

Empty є ≼ є

Char c ≼ c

Seq p1 ≼ m1           p2 ≼ m2 p1p2 ≼ m1m2

OrLeft p1 ≼ m p1|p2 ≼ m

OrRight p2 ≼ m p1|p2 ≼ m

StarEmpty p* ≼ є

StarSeq p ≼ m1           p* ≼ m2 p* ≼ m1m2

---

La définition de p ≼ m est faite selon le formalisme des règles d’inférence, qui est très courant. Il permet la définition inductive d’un prédicat. Les règles se décomposent en axiomes (par ex. Empty) qui sont les cas de base de la définition, et en règles d’inférence proprement dites qui sont les cas inductifs de la définition. Les règles sont à comprendre comme des implications : quand toutes les prémisses (au dessus du trait) sont vraies, alors la conclusion (au dessous du trait) est vraie. En enchaînant les règles on obtient une preuve effective du prédicat, appelée arbre de dérivation. Voici par exemple la preuve de ab*|ba* ≼ baa.

Nous disposons donc de deux moyens d’exprimer un langage régulier, m ∈ [[p]] ou p ≼ m. Selon les circonstances, il est plus facile d’employer l’un ou l’autre de des moyens. Par exemple, pour montrer qu’un motif filtre un mot, les règles d’inférences sont souvent commodes. En revanche, pour montrer des égalités de langages réguliers, il est souvent plus commode de se servir des opérations sur les langages.

6.2  Notations supplémentaires

En pratique on rencontre diverses notations qui peuvent toutes être exprimées à l’aide des constructions de base des expressions régulières. Autrement dit, l’emploi de ces notations n’augmente pas la classe des langages réguliers, mais permet simplement d’écrire des expressions régulières plus compactes.

• Le motif optionnel p? défini comme p|є.
• La répétition au moins une fois p+ définie comme pp*.
• Le joker, noté ., qui est l’alternative de tous les caractères de Σ. On a donc [[.]] = Σ.

Il existe également toute une variété de notations pour des ensembles de caractères. Ces motifs sont des abréviations de l’alternative notées entre crochets […]. Donc, au sein de ces crochets, on trouve une suite des classes de caractères suivantes :

• Un caractère c se représente lui-même.
• Un intervalle c₁-c₂ représente les caractères dont les codes sont compris au sens large entre les codes de c₁ et c₂.

La notation [^…] se comprend comme le complémentaire des classes de caractères données. Il est clair que les notations de classes de caractères peuvent s’exprimer comme des alternatives de motifs caractères. Dans le cas du complémentaire, cela suppose un alphabet Σ fini, ce qui est bien évidemment le cas en pratique.

Enfin certains caractères spéciaux sont exprimables à l’aide de notations assez usuelles, du style \n est le caractère fin de ligne et \t est la tabulation etc. Le caractère barre oblique inverse (backslash) introduit les notations de caractères spéciaux, mais permet aussi d’exprimer les caractères actifs des expressions régulières comme eux-mêmes, c’est à dire de les citer. Par exemple le caractère étoile se note \* et, bien évidemment, le caractère barre oblique inverse se note \\. Il n’est pas l’usage de citer les caractères quand c’est inutile, ainsi [^*] représente tous les caractères sauf l’étoile.

//Commentaire avant
i++ ;

6.3  Programmation avec les expressions régulières

Dans cette section nous nous livrons à une description rapide de quelques outils qui emploient les expressions régulières de façon cruciale. Le sujet est extrêmement vaste, car le formalisme des expressions régulières est suffisamment expressif pour permettre de nombreuses recherches dans les fichiers textes, voire de nombreuses transformations de ces fichiers. Le livre de Jeffrey E. F. Friedl [3] traite des expressions régulière du point de vue des outils.

6.3.1  Dans l’interprète de commandes Unix

Le shell c’est à dire l’interprète de commandes Unix reconnaît quelques expressions régulières qu’il applique aux noms des fichiers du répertoire courant. La syntaxe concrète des motifs est franchement particulière. Notons simplement que ? représente un caractère quelconque (noté précédemment .), tandis que * représente un mot quelconque (noté précédemment .*), et que l’alternative se note à peu près {p₁,p₂} (pour p₁|p₂)…

Ainsi, on pourra effacer tous les fichiers objets Java par la commande :

% /bin/rm *.class

Dans le même ordre d’idée, on peut compter toutes les lignes des fichiers source du répertoire courant :

% wc -l *.java

La commande wc¹ (pour word count) compte les lignes, mots et caractères dans les fichiers donnés en argument. L’option « -l » restreint l’affichage au seul compte des lignes. Enfin, on peut faire la liste de tous les fichiers du répertoire courant dont le nom comprend de un à trois caractères :

% ls {?,??,???}

6.3.2  Recherche de lignes dans un fichier, la commande egrep

La commande egrep motif fichier affiche toutes les lignes de fichier dont motif filtre un sous-mot (et non pas la ligne entière). La syntaxe des motifs est relativement conforme à ce que nous avons déjà décrit. Supposons, comme c’est souvent le cas, que le fichier /usr/share/dict/french de votre machine Unix est un dictionnaire français, donné sous forme d’un fichier texte, à raison d’un mot par ligne. On peut alors trouver les mots qui contiennent au moins six fois la lettre « i » de cette manière.

% egrep 'i.*i.*i.*i.*i.*i' /usr/share/dict/french 
indivisibilité

On notera que l’argument motif est donné entre simples quotes « ' », ceci afin d’éviter que le shell n’interprète les étoiles comme faisant partie d’un motif à appliquer aux noms de fichier. Ce n’est en fait pas toujours nécessaire, mais c’est toujours prudent.

6.3.3  En Java

Le support pour les expressions régulières est assuré par les classes Pattern et Matcher du package java.util.regexp, Les objets de la classe Pattern implémentent les motifs. et sont construits par la méthode statique Pattern.compile qui prend une chaîne représentant un motif en argument et renvoie un Pattern. On pourrait penser que la méthode compile interprète la chaîne donnée en argument et produit un arbre de syntaxe abstraite. En fait, par souci d’efficacité, elle procède à bien plus de travail, jusqu’à produire un automate (voir le chapitre suivant). Pour le moment, il suffit de considérer qu’un Pattern est la forme Java d’un motif.

Pour confronter un Pattern p à un mot m il faut fabriquer cette fois un Matcher en invoquant la méthode matcher(String text) de p, l’argument text étant le mot m. En simplifiant, le Matcher obtenu est donc la combinaison d’un motif p et d’un mot m, il offre (entre autres !) les méthodes matches() et find() qui renvoient des booléens. La première méthode matches teste si le motif p filtre le mot m, tandis que la seconde find teste si le motif p filtre un sous-mot du mot m. Ainsi, par exemple, un moyen assez compliqué de savoir si un mot mot contient le sous-mot sous au moins deux fois est d’écrire :

Nous en savons maintenant assez pour pouvoir écrire la commande egrep en Java, la classe Grep dont le code est donné à la figure 6.5 (source Grep.java).

---

Figure 6.5: La commande egrep en Java, source Grep.java

import java.io.* ;         // Pour  BufferedReader
import java.util.regex.* ; // Pour Pattern et Matcher

class Grep {

  // Affiche les lignes de in dont un sous-mot est filtré par le motif p  
  static void grep(String p, BufferedReader in) throws IOException {
    Pattern pat = Pattern.compile(p) ;
    String line = in.readLine() ;
    while (line != null) {
      Matcher m = pat.matcher(line) ;
      if (m.find()) {
        System.out.println(line) ;
      }
      line = in.readLine() ;
    }
  }

  public static void main(String [] arg) {
    if (arg.length != 2) {
      System.err.println("Usage: java Grep motif fichier") ;
      System.exit(2) ;
    }
    try {
      BufferedReader in = new BufferedReader (new FileReader (arg[1])) ;
      grep(arg[0], in) ;
      in.close() ;
    } catch (IOException e) {
      System.err.println("Malaise: " + e.getMessage()) ;
      System.exit(2) ;
    }
  }
}

---

Dans ce code, la méthode main se comporte principalement ainsi : elle ouvre le fichier dont le nom est donné comme second argument de la ligne de commande, par new FileReader(arg[1]) ; puis enveloppe le fichier comme le BufferedReader (voir B.6.2.2) in, ceci afin de pouvoir le lire ligne à ligne ; enfin le code appelle la méthode grep. Cette dernière, après construction du Pattern pat, l’applique à toutes les lignes du fichier. En cas de succès de l’appel à find, la ligne est affichée sur la sortie standard. Le comportement global est donc bien celui de la commande egrep.

L’architecture du package java.util.regex peut paraître bien compliquée, et c’est tout à vrai. Mais…

• L’existence de la classe Pattern se justifie d’abord par le souci d’abstraction : les auteurs ne souhaitent pas exposer comment sont implémentés les motifs, afin de pouvoir changer cette implémentation dans les versions futures de Java. Il y a également un souci d’efficacité, la transformation des chaînes vers les motifs est coûteuse et on souhaite la rentabiliser. Par exemple dans notre Grep (figure 6.5), nous appelons Pattern.compile une seule fois et pratiquons de nombreux filtrages.
• L’existence de la classe Matcher s’explique autrement : les Matcher possèdent un état interne que les méthodes de filtrage modifient. Ceci permet d’abord d’obtenir des informations supplémentaires. Par exemple, si find réussit, alors on obtient le sous-mot filtré en appelant la méthode group(). Par ailleurs, l’appel suivant à find recherchera un sous-mot filtré, non plus à partir du début, mais au delà du dernier sous-mot identifié par find. Tout cela permet par exemple d’extraire tous les entiers présents dans une chaîne.
  static void allInts(String text) {
    Matcher m = Pattern.compile("[0-9]+").matcher(text) ;
    while (m.find()) {
      System.out.println(m.group()) ;
    }
  }
  On notera qu’il n’est pas immédiat que le code ci-dessus affiche bien tous les entiers de la chaîne text. En effet si text est par exemple "12" les deux affichages 12, ou encore 1 puis 2 sont corrects : il n’affichent que des sous-mots filtrés par le motif "[0-9]+".

  Plus généralement, spécifier complètement ce que fait le couple de méthode find/group est un peu délicat. La solution à mon avis la plus satisfaisante est spécifier que le sous-mot filtré est d’abord le plus à gauche et ensuite le le plus long. La spécification de Java n’est pas aussi générale : au lieu de dire globalement ce qui doit être filtré, elle décrit l’effet de chaque opérateur des expressions régulière individuellement. Ici elle dit que l’opérateur « + » est avide (greedy), c’est à dire qu’il filtre le plus de caractères possibles. Dans le cas de l’expression régulière simple "[0-9]+", cela revient en effet à filtrer les sous-mots les plus longs.

Nous ne décrirons pas plus en détail les expressions régulières de Java. La documentation du langage offre de nombreuses précisions. En particulier, la documentation de la classe Pattern comprend la description complète de la syntaxe des motifs qui est plus étendue que ce que nous avons vu ici. Attention tout de mêmes les descriptions de motifs sont données dans l’absolu, alors que les motifs sont souvent en pratique dans des chaînes. If faut donc en plus tenir compte des règles de citation dans les chaînes. Ainsi le motif \p{L} filtre n’importe quelle lettre (y compris les lettres accentuées) mais on le donne sous la forme de la chaîne "\\p{L}", car il faut citer un backslash avec un backslash !

6.4  Implémentation des expressions régulières

Le but de cette section est de décrire une technique d’implémentation possible des expressions régulières en Java. Il s’agit d’une première approche, beaucoup moins sophistiquée que celle adoptée notamment par la bibliothèque Java. Toutefois, on pourra, même avec des techniques simples, déjà aborder les problèmes de programmation posés et comprendre « comment ça marche ». De fait nous allons imiter l’architecture du package java.util.regexp et écrire nous aussi un package que nous appelons regex tout court.

Nous en profitons donc pour écrire un package. Tous les fichiers source du package regex commencent par la ligne package regex ; qui identifie leur classe comme appartenant à ce package. En outre, il est pratique de regrouper ces fichiers dans un sous-répertoire nommé justement regex. Le source du nouveau package est disponible comme l’archive regex.tar qui contient regex/Flux.java (non décrit), regex/Re.java (arbre de syntaxe abstraite, section 6.4.1), regex/Pattern.java (section 6.4.2) et regex/Matcher.java (section 6.4.3).

6.4.1  Arbres de syntaxe abstraite

Nous reprenons les techniques de la section 4.4 sur les arbres de syntaxe abstraite. À savoir nous définissons une classe Re des nœuds de l’arbre de syntaxe abstraite.

Nous définissons cinq sortes de nœuds, la sorte d’un nœud étant identifiée par son champ tag. Des constantes nommées identifient les cinq sortes de nœuds. La correspondance entre constante et sorte de nœud est directe, on note la présence de nœuds « WILD » qui représentent les jokers. Ensuite nous définissons tous les champs nécessaires, un champ asChar utile quand le motif est un caractère (tag CHAR), et deux champs p1 et p2 utiles pour les nœuds internes qui ont au plus deux fils. Enfin, le constructeur par défaut est redéfini et déclaré privé.

On construira les divers nœuds en appelant des méthodes statiques bien nommées. Par exemple, pour créer un motif caractère, on appelle :

Pour créer un motif répétition, on appelle :

Les autres autres méthodes de construction sont évidentes.

Les méthodes statiques de construction ne se limitent évidemment pas à celles qui correspondent aux sortes de nœuds existantes. On peut par exemple écrire facilement une méthode plus qui construit un motif p+ comme pp*.

Du point de vue de l’architecture, on peut remarquer que tous les champs et le constructeur sont privés. Rendre le constructeur privé oblige les utilisateurs de la classe Re appeler les méthodes statiques de construction, de sorte qu’il est garanti que tous les champs utiles dans un nœud sont correctement initialisés. Rendre les champs privés interdira leur accès de l’extérieur de la classe Re. Au final, la politique de visibilité des noms est très stricte. Elle renforce la sécurité de la programmation, puisque si nous ne modifions pas les champs dans la classe Re, nous pourrons être sûrs que personne ne le fait. En outre, la classe Re n’est pas publique, son accès est donc limité aux autres classes du package regex. La classe Re est donc complètement invisible pour les utilisateurs du package.

6.4.2  Fabrication des expressions régulières

Nous présentons maintenant notre classe Pattern, un modeste remplacement de la classe homonyme de la bibliothèque Java. Pour le moment nous évitons les automates et nous contentons de cacher un arbre Re dans un objet de la classe Pattern.

Comme dans la classe de la bibliothèque, c’est la méthode statique compile qui appelle le constructeur, ici privé. La partie la plus technique de la tâche de la méthode compile est le passage de la syntaxe concrète contenue dans la chaîne patString à la syntaxe abstraite représenté par un arbre Re, opération déléguée à la méthode Re.parse. Nous ne savons pas écrire cette méthode d’analyse syntaxique (parsing). (cours INF 431). Mais ne soyons pas déçus, nous pouvons déjà par exemple construire le motif qui reconnaît au moins k caractères c, en appelant la méthode atLeast suivante, à ajouter dans la classe Pattern.

Enfin, la méthode matcher de de la classe Pattern se contente d’appeler le constructeur de notre modeste classe Matcher, que nous allons décrire.

6.4.3  Filtrage

---

Figure 6.6: Notre classe Matcher

package regex ;

public class Matcher {
  private Re pat ;
  private String text ;

  // Les recherches commencent à cette position dans text
  private int regStart ;
  // La dernière sous-chaîne filtrée est text[mStart...mEnd[
  private int mStart, mEnd ;

  Matcher(Re pat, String text) {
    this.pat = pat ; this.text = text ;
    regStart = 0 ;       // Commencer à filtrer à partir du début
    mStart = mEnd = -1 ; // Aucun motif encore reconnu
  }

  // Renvoie la dernière sous-chaîne filtrée, si il y a lieu
  public String group() {
    if (mStart == -1) throw new Error("Pas de sous-chaîne filtrée") ;
    return text.substring(mStart, mEnd) ;
  }

  // Méthode de recherche des sous-chaînes filtrées a peu près
  // conforme à celle des Matcher de java.util.regex
  public boolean find() {
    for (int start = regStart ; start <= text.length() ; start++)
      for (int end = text.length() ; end >= start ; end--) {
        if (Re.matches(text, pat, start, end)) {
          mStart = start ; mEnd = end ;
          regStart = mEnd ; // Le prochain find commencera après celui-ci
          return true ;
        }
      }
    mStart = mEnd = -1 ; // Pas de sous-chaîne reconnue
    regStart = 0 ;       // Recommencer au début, bizarre
    return false ;
  }
}

---

Le source de la classe Matcher (figure 6.6) indique que les objets contiennent deux champs pat et text, pour le motif et le texte à filtrer. Comme on pouvait s’y attendre, le constructeur Matcher(Re pat, String text) initialise ces deux champs. Mais les objets comportent trois champs supplémentaires, mStart, mEnd et regStart.

• La valeur du champ regStart indique l’indice dans text du début de la recherche suivante, c’est-à-dire où la méthode find doit commencer à chercher une sous-chaîne filtrée par pat. Ce champ permet donc aux appels successifs de find de communiquer entre eux.
• Les champs mStart et mEnd identifient la position de la dernière sous-chaîne de text dont un appel à find a déterminé que le motif pat la filtrait. La convention adoptée est celle de la méthode substring des objets String (voir la section B.6.1.3). Les deux champs servent à la communication entre un appel à find et un appel subséquent à group (voir la fin de la section 6.3.3).

La méthode find est la plus intéressante, elle cherche à identifier une sous-chaîne filtrée par pat, à partir de la position regStart et de la gauche vers la droite. La technique adoptée est franchement naïve, on essaie tout simplement de filtrer successivement toutes les sous-chaînes commençant à une positon donnée (start) des plus longues à la chaîne vide. On renvoie true (après mise à jour de l’état du Matcher), dès qu’une sous-chaîne filtrée est trouvée. Pour savoir si une sous-chaîne text[start…end[ est filtrée, on fait appel à la méthode statique Re.matches. Notons que c’est notre parti-pris de rendre privés tous les champs de l’arbre de syntaxe des expressions régulière qui oblige à écrire toute méthode qui a besoin d’examiner cette structure comme une méthode de la classe Re.

Pour écrire la méthode matches de la classe Re, nous allons distinguer les divers motifs possibles et suivre la définition de p ≼ m de la figure 6.3.

Notons bien que text[i…j[ est la chaîne dont nous cherchons à savoir si elle est filtrée par pat. La longueur de cette chaîne est j-i. Nous écrivons maintenant le source du traitement des cinq sortes de motifs possibles, c’est à dire la liste des cas du switch ci-dessus. Le cas des motifs vide, des caractères et du joker est rapidement réglé.

En effet, le motif vide filtre la chaîne vide et elle seule (j−i = 0), le motif caractère ne filtre que la chaîne composée de lui même une fois, et le joker filtre toutes les chaînes de longueur un.

Le cas de l’alternative est également assez simple, il suffit d’essayer les deux termes de l’alternative (regles OrLeft et OrRight).

La séquence (rule Seq) demande plus de travail. En effet il faut essayer toutes les décompositions en préfixe et suffixe de la chaîne testée, faute de quoi nous ne pourrions pas renvoyer false avec certitude.

Et enfin, le cas de la répétition q* est un peu plus subtil, il est d’abord clair (règle StarEmpty) qu’un motif q* filtre toujours la chaîne vide. Si la chaîne text[i…j[ est non-vide alors on cherche à la décomposer en préfixe et suffixe et à appliquer la règle StarSeq.

On note un point un peu subtil, dans le cas d’une chaîne non-vide, on évite le cas k = j qui correspond à une division de la chaîne testée en préfixe vide et suffixe complet. Si tel n’était pas le cas, la méthode matches pourrait ne pas terminer. En effet, le second appel récursif matches(text, pat, k, j) aurait alors les mêmes arguments que lors de l’appel. Un autre point de vue est de considérer que l’application de la règle StarSeq à ce cas est inutile, dans le sens qu’on ne risque pas de ne pas pouvoir prouver q* ≼ m parce que l’on abstient de l’employer.

L’inutilité de cette règle est particulièrement flagrante, puisqu’une des prémisses et la conclusion sont identiques.

6.4.4  Emploi de notre package regex

Nos classes Pattern et Matcher sont suffisamment proches de celles de la bibliothèque pour que l’on puisse, dans le source Grep.java (figure 6.5), changer la ligne import java.util.regex.* en import regex.*, ce qui nous donne le nouveau source ReGrep.java. Dès lors, à condition que le source des classes du package regex se trouve dans un sous-répertoire regex, nous pouvons compiler par javac ReGrep.java et nous obtenons un nouveau programme ReGrep qui utilise notre implémentation des expressions régulières à la place de celle de la bibliothèque.

Nous nous livrons ensuite à des expériences en comparant les temps d’exécution (par les commandes time java Grep … et time java ReGrep …).

1. Dans le dictionnaire français, nous recherchons les mots qui contiennent au moins n fois la même voyelle non accentuée. Par exemple, pour n = 3 nous exécutons la commande :

   % java Grep '(a.*a.*a|e.*e.*e|i.*i.*i|o.*o.*o|u.*u.*u)' /usr/share/dict/french
   

   	1	2	3	4	5	6
   Grep	2.7	2.5	1.9	1.7	1.6	1.5
   ReGrep	3.1	9.7	16.4	17.9	18.6	18.0

   On voit que notre technique, sans être ridicule, est nettement moins efficace.
2. Toujours dans le dictionnaire français, nous recherchons les mots qui contiennent n fois la lettre e, après effacement des accents. Par exemple, pour n = 3 nous exécutons la commande :

   % java Grep '(e|é|è|ê).*(e|é|è|ê).*(e|é|è|ê)' /usr/share/dict/french
   

   	1	2	3	4	5	6	7
   Grep	2.9	2.2	1.9	1.7	1.6	1.5	1.5
   ReGrep	3.1	9.0	12.8	15.2	15.8	16.0	15.9

   Cette expérience donne des résultats similaires à la précédente. Plus précisément d’une part la bibliothèque est plus rapide en valeur absolue ; et d’autre part, nos temps d’exécution sont croissants, tandis que ceux de la bibliothèque sont décroissants. Mais et c’est important, il semble bien que les temps se stabilisent dans les deux cas.
3. Nous recherchons une sous-chaîne filtrée par X(.+)+X dans la chaîne XX=⋯=, où =⋯= est le caractère = répété n fois. Cette reconnaissance doit échouer, mais nous savons [3, Chapitre 5] qu’elle risque de mettre en difficulté l’implémentation de la bibliothèque.

   	16	18	20	22	24
   Grep	0.3	0.5	1.3	4.8	18.6
   ReGrep	0.2	0.2	0.2	0.2	0.2

   Et effectivement l’emploi de la bibliothèque conduit à un temps d’exécution manifestement exponentiel. Il est fascinant de constater que notre implémentation ne conduit pas à cette explosion du temps de calcul.

6.5  Une autre approche du filtrage

6.5.1  Langage dérivé

Soit L un langage sur les mots et c un caractère. Nous notons c⁻¹·L le langage dérivé, défini comme les suffixes m des mots de L qui sont de la forme c·m.

Dans le cas d’un langage L régulier engendré par le motif p, nous allons montrer que le langage c⁻¹·L est régulier en calculant le motif c⁻¹·p qui l’engendre.

On observera d’abord que, en toute rigueur, le langage c⁻¹·L peut être vide, par exemple si L = { c′ } avec c′ ≠ c. Or, selon notre définition des langages réguliers, le langage vide ∅ n’est pas régulier. Qu’à cela ne tienne, nous inventons immédiatement un nouveau motif ∅, qui ne filtre aucun mot. En considérant les valeurs [[p]], on étend facilement les trois opérateurs des expressions régulières.

Ces règles nous permettent d’éliminer les occurrences internes de ∅, de sorte qu’un motif est désormais ∅ ou un motif qui ne contient pas ∅.

Par ailleurs, on décide de la validité de p ≼ є par une simple induction structurelle.

6.5.2  Filtrage par la dérivation des motifs

Pour savoir si un motif p filtre un mot m, on peut tout simplement itérer sur les caractères du mot, en calculant les dérivations successives de p par les caractères consommés. Un fois atteint la fin du mot, il ne reste qu’à vérifier si le motif dérivé filtre le mot vide.

Plus précisément, les deux résultats de la section précédente (proposition 15 et lemme 16) nous permettent d’écrire deux nouvelles méthodes statiques dans la classe Re.

On peut alors écrire par exemple la méthode matches (simplifiée, sans tenir compte de mStart et mEnd) de la classe Matcher ainsi :

La mesure des temps d’exécution de la nouvelle classe Matcher fait apparaître de meilleurs performances dans les deux premières expériences de la section 6.4.4 et une consommation très importante de la mémoire dans la dernière expérience.

1

On obtient le détail du fonctionnement d’une commande Unix cmd par man cmd.